L06 MDP in Finance

DO NOT DISTRIBUTE.

• L06 MDP in Finance
  • MDP Theory
    • Introduction
      • Introduction
      • Applications: Consumption Problem
      • A Reference Book
    • Markov Decision Models
      • Defining A Markov Decision Models
      • An equivalent definition of MDP
      • Example: Consumption Problem
    • Finite Horizon Markov Decision Models
      • Finite Horizon Markov Decision Models
    • The Bellman Equation
      • The Bellman Equation
      • Reward Iteration
      • Maximizer, the Bellman Equation & Verification Theorem
      • The Structure Assumption & Structure Theorem
  • The Financial Markets
    • Asset Dynamics and Portfolio Strategies
      • Asset Dynamics and Portfolio Strategies
    • Modeling and Solution Approaches with MDP
      • Modeling and Solution Approaches with MDP
  • MDP Applications in Finance
    • A Cash Balance Problem
      • A Cash Balance Problem
      • Problem Formulation
      • Solution
    • Consumption and Investment Problems
      • Consumption and Investment Problems
      • Formulation
      • Solution
    • Terminal Wealth Problems
      • Terminal Wealth Problems
      • Formulation
      • Solution
    • Portfolio Selection with Transaction Costs
      • Portfolio Selection with Transaction Costs
      • Formulation
    • Dynamic Mean-Variance Problems
      • Dynamic Mean-Variance Problems
      • Formulation
    • Index Tracking
      • Index Tracking
      • Formulation

MDP Theory

Introduction

Introduction

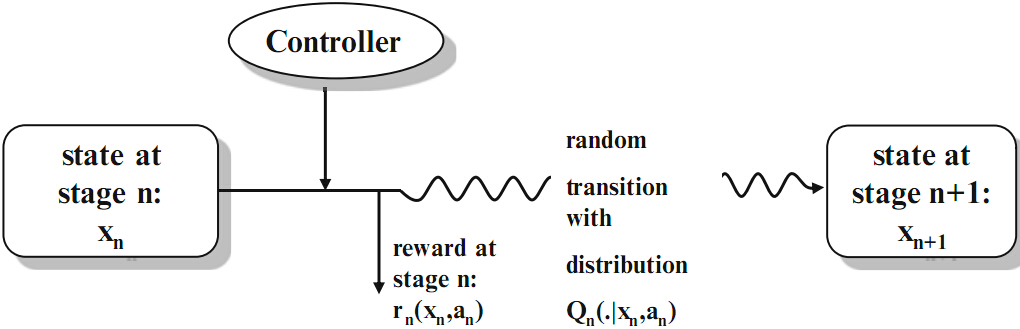
The Markov Decision Process is the sequence of random variables ($X_n$) which describes the stochastic evolution
of the system states. Of course the distribution of ($X_n$) depends on the chosen actions.

• $E$ denotes the state space of the system. A state $x\in E$ is the information which is available for the controller at time $n$. Given this information an action has to be selected.

• $A$ denotes the action space. Given a specific state $x\in E$ at time $n$, a certain subclass $D_n(x)\subset A$ of actions may only be admissible.

• $Q_n(B|x,a)$ is a stochastic transition kernel which gives the probability that the next state at time $n+1$ is in the set B if the current state is $x$ and action a is taken at time $n$.

• $r_n(x, a)$ gives the (discounted) one-stage reward of the system at time $n$ if the current state is $x$ and action a is taken

• $g_N(x)$ gives the (discounted) terminal reward of the system at the end of the planning horizon.

---

A control $\pi$ is a sequence of decision rules ($f_n$) with $f_n:E\rightarrow A$ where $f_n(x)\in D_n(x)$ determines for each possible state $x\in E$ the next action $f_n(x)$ at time $n$. Such a sequence $\pi=(f_n)$ is called policy or strategy. Formally the Markov Decision Problem is given by

$$V_0(x)=\sup_{\pi}\mathbb{E}_x^{\pi}\left[\sum_{k=0}^{N-1}r_k\left(X_k,f_k(X_k)\right)+g_N(X_N)\right],\text{ }x\in E.$$

• Types of MDP problems:

  • finite horizon ($N<\infty$) vs. infinite horizon ($N=\infty$)
  • complete state observation vs. partial state observation
  • problems with constraints vs. without constraints
  • total (discounted) cost criterion vs. average cost criterion

• Research questions:

  • Does an optimal policy exist?
  • Has it a particular form?
  • Can an optimal policy be computed efficiently?
  • Is it possible to derive properties of the optimal value function analytically?

---

Applications: Consumption Problem

• Consumption Problem
  Suppose there is an investor with given initial capital. At the beginning of each of $N$ periods she can decide how much of the capital she consumes and how much she invests into a risky asset. The amount she consumes is evaluated by a utility function $U$ as well as the terminal wealth. The remaining capital is invested into a risky asset where we assume that the investor is small and thus not able to influence the asset price and the asset is liquid. How should she consume/invest in order to maximize the sum of her expected discounted utility?

• Cash Balance or Inventory Problem
  Imagine a company which tries to find the optimal level of cash over a finite number of $N$ periods. We assume that there is a random stochastic change in the cash reserve each period (due to withdrawal or earnings). Since the firm does not earn interest from the cash position, there are holding cost for the cash reserve if it is positive, but also interest (cost) in case it is negative. The cash reserve can be increased or decreased by the management at each decision epoch which implies transfer costs. What is the optimal cash balance policy?

• Mean-Variance Problem
  Consider a small investor who acts on a given financial market. Her aim is to choose among all portfolios which yield at least a certain expected return (benchmark) after $N$ periods, the one with smallest portfolio variance. What is the optimal investment strategy?

• Dividend Problem in Risk Theory
  Imagine we consider the risk reserve of an insurance company which earns some premia on the one hand but has to pay out possible claims on the other hand. At the beginning of each period the insurer can decide upon paying a dividend. A dividend can only be paid when the risk reserve at that time point is positive. Once the risk reserve got negative we say that the company is ruined and has to stop its business. Which dividend pay-out policy maximizes the expected discounted dividends until ruin?

• Bandit Problem
  Suppose we have two slot machines with unknown success probability $\theta_1$ and $\theta_2$. At each stage we have to choose one of the arms. We receive one Euro if the arm wins, else no cash flow appears. How should we play in order to maximize our expected total reward over $N$ trials?

• Pricing of American Options
  In order to find the fair price of an American option and its optimal exercise time, one has to solve an optimal stopping problem. In contrast to a European option the buyer of an American option can choose to exercise any time up to and including the expiration time. Such an optimal stopping problem can be solved in the framework of Markov Decision Processes.

A Reference Book

You may buy it via Amazon, or find it via Springer Link

---

Markov Decision Models

Defining A Markov Decision Models

Markov Decision Model with planning horizon $N\in\mathbb{N}$ consists of a set of data $(E,A,D_n,Q_n,r_n,g_N)$ with the following meaning for $n =0,1,2,\dots,N-1$:

• $E$ is the state space, endowed with a $\sigma$-algebra $\mathfrak{E}$. The elements (states) are denoted by $x\in E$

• $A$ is the action space, endowed with a $\sigma$-algebra $\mathfrak{A}$. The elements (actions) are denoted by $a\in A$

• $D_n\subset E\times A$ is a measurable subset of $E\times A$ and denotes the set of possible state-action combinations at time $n$. We assume that $D_n$ contains the graph of a measurable mapping $f_n:E\rightarrow A$, i.e. $(x, f_n(x))\in D_n$ for all $x\in E$. For $x\in E$,the set $D_n(x)= \{a\in A: (x,a)\in D_n\}$ is the set of admissible actions in state $x$ at time $n$.

• $Q_n$ is a stochastic transition kernel from $D_n$ to $E$, i.e. for any fixed pair $(x, a)\in D_n$, the mapping $B\mapsto Q_n(B|x, a)$ is a probability measure on $\mathfrak{E}$ and $(x, a)\mapsto Q_n(B|x, a)$ is measurable for all $B\in \mathfrak{E}$.The quantity $Q_n(B|x, a)$ gives the probability that the next state at time $n + 1$ is in $B$ if the current state is $x$ and action a is taken at time $n$. $Q_n$ describes the **transition law}.

• $r_n: D_n\rightarrow R$ is a measurable function. $r_n(x, a)$ gives the (discounted) one-stage reward of the system at time $n$ if the current state is $x$ and action a is taken.

• $g_N:E\rightarrow R$ is a measurable mapping. $g_N(x)$ gives the (discounted) terminal reward of the system at time $N$ if the state is $x$.

---

An equivalent definition of MDP

A Markov Decision Model is equivalently described by the set of data $(E,A,D_n,Z,T_n,Q^Z_n ,r_n,g_N)$ with the following meaning:

• $E,A,D_n,r_n,g_N$ are as in Definition of last slide

• $Z$ is the disturbance space, endowed with a $\sigma$-algebra $\mathfrak{Z}$.

• $Q^Z_n (B|x, a)$ is a stochastic transition kernel for $B\in Z$ and $(x, a)\in D_n$ and $Q^Z_n (B|x, a)$ denotes the probability that $Z_{n+1}$ is in $B$ if the current state is $x$ and action $a$ is taken.

• $T_n : D_n\times Z\rightarrow E$ is a measurable function and is called transition or system function. $T_n(x, a, z)$ gives the next state of the system at time $n+1$ if at time $n$ the system is in state $x$,action $a$ is taken and the disturbance $z$ occurs at time $n +1$.

---

Example: Consumption Problem

We denote by $Z_{n+1}$ the random return of our risky asset over period $[n, n+1)$. Further we suppose that $Z_1,\dots,Z_N$ are non-negative, independent random variables and we assume that the consumption is evaluated by utility functions $U_n:\mathbb{R}_+\rightarrow \mathbb{R}$. The final capital is also evaluated by a utility function $U_N$. Thus we choose the following data:

• $E = \mathbb{R}_+$ where $x_n\in E$ denotes the wealth of the investor at time $n$

• $A = \mathbb{R}_+$ where $a_n \in A$ denotes the wealth which is consumed at time $n$

• $D_n(x)=[0,x]$ for all $x\in E$, i.e. we are not allowed to borrow money

• $Z =\mathbb{R}_+$ where $z$ denotes the random return of the asset

• $T_n(x_n,a_n,z_{n+1})=(x_n-a_n)z_{n+1}$ is the transition function

• $Q^Z_n (\cdot|x, a) =$ distribution of $Z_{n+1}$ (independent of $(x, a)$)

• $r_n(x, a)= U_n(a)$ is the one-stage reward

• $g_N(x)= U_N(x)$

• Decision rule & strategy

  • A measurable mapping $f_n : E\rightarrow A$ with the property $f_n(x)\in D_n(x)$ for all $x\in E$, is called a decision rule at time $n$. We denote by $F_n$ the set of all decision rules at time $n$.

  • A sequence of decision rules $\pi =(f_0,f_1,\dots,f_{N-1})$ with $f_n\in F_n$ is called an $N$-stage policy or $N$-stage strategy.

• Value function:
  $$V_n(x)=\sup_{\pi}V_{n\pi}(x),\ x\in E.$$

• A theorem: For $n=0,\dots,N$ it holds:
  $$V_n(x_n)=\sup_{\pi\in\Pi_N}V_{n\pi}(h_n),\text{ }h_n=(x_0,a_0,x_1,\dots,x_n).$$

---

Finite Horizon Markov Decision Models

Finite Horizon Markov Decision Models

**Integrability Assumption ($A_N$):} For $n=0,1,\dots,N$
$$\delta^N_n(x)=\sup_{\pi}\mathbb{E}_{nx}^{\pi}\left[\sum_{k=n}^{N-1}r_k^+(X_k,f_k(X_k))+g_N^+(X_N)\right]<\infty,\text{ }x\in E.$$
Assumption ($A_N$) is assumed to hold for the $N$-stage Markov Decision Problems.

Example: (Consumption Problem) In the consumption problem Assumption ($A_N$) is satisfied if we assume that the utility functions are increasing and concave and $\mathbb{E} Z_n < \infty$ for all $n$, because then $r_n$ and $g_N$ can be bounded by an affine-linear function $c_1 + c_2x$ with $c_1, c_2 \geq 0$ and since $X_n \leq xZ_1 \dots Z_n$ a.s. under every policy, the function $\delta_n^N$ satisfies
$$\begin{array}{lll} \delta^N_n(x)&=&\sup_{\pi}\mathbb{E}_{nx}^{\pi}\left[\sum_{k=n}^{N-1}U_k^+(f_k(X_k))+U_N^+(X_N)\right]\\ &\leq&Nc_1+xc_2\sum_{k=n}^N\mathbb{E}Z_1\dots\mathbb{E}Z_k<\infty,\text{ }x>0 \end{array}$$

For $n = 0, 1,\dots, N$ and a policy $\pi = (f_0,\dots, f_{N-1})$ let $V_{n\pi}(x)$ be defined by
$$V_{n\pi}(x)=\mathbb{E}_{nx}^{\pi}\left[\sum_{k=n}^{N-1}r_k(X_k,f_k(X_k))+g_N(X_N)\right],\text{ }x\in E.$$
$V_{n\pi}(x)$ is the expected total reward at time $n$ over the remaining stages $n$ to $N$ if we use policy $\pi$ and start in state $x\in E$ at time $n$. The value function $V_n$ is defined by
$$V_n(x)=\sup_{\pi}V_{n\pi}(x),\text{ }x\in E.$$
$V_n(x)$ is the maximal expected total reward at time $n$ over the remaining stages $n$ to $N$ if we start in state $x\in E$ at time $n$. The functions $V_{n\pi}$ and $V_n$ are well-defined since
$$V_{n\pi}(x)\leq V_{n}(x)\leq\delta_n^N(x)<\infty,\text{ }x\in E.$$

---

The Bellman Equation

The Bellman Equation

Let us denote by $\mathbb{M}(E)=\{v\in E\mapsto[-\infty,\infty)| v\text{ is measurable}\}$, we define the following operators:

• [ For $v\in \mathbb{M}(E)$ define
  $$(L_nv)(x,a)=r_n(x,a)+\int v(x')Q_n(dx'|x,a),\text{ }(x,a)\in D_n$$
  whenever the integral exists.

• For $v\in \mathbb{M}(E)$ and $f\in F_n$ define
  $$(\mathcal{T}_{nf}v)(x)=(L_nv)(x,f(x)),\text{ }x\in E.$$

• [ For $v\in \mathbb{M}(E)$ define
  $$(\mathcal{T}_{n}v)(x)=\sup_{a\in D_n(x)}(L_nv)(x,a),\text{ }x\in E.$$
  $\mathcal{T}_n$ is called the maximal reward operator at time $n$.

---

Reward Iteration

Theorem
Let $\pi=(f_0,\dots,f_{N-1})$ be an $N$-stage policy. For $n=0,1,\dots,N-1$ it holds:

• $V_{N\pi}=g_N$ and $V_{n\pi}=\mathcal{T}_{nf_n}V_{n+1,\pi}$,
• $V_{n\pi}=\mathcal{T}_{nf_n}\dots\mathcal{T}_{N-1f_{N-1}}g_N$.

Example: (Consumption Problem) Note that for $f_n\in F_n$ the $\mathcal{T}_{nf_n}$ operator in this example reads
$$\mathcal{T}_{nf_n}=U_n(f_n(x))+\mathbb{E}v\left(\left(x-f_n\left(x\right)\right)Z_{n+1}\right).$$
Now let us assume that $U_n(x) = \log x$ for all $n$ and $g_N(x) = \log x$. Moreover, we assume that the return distribution is independent of $n$ and has finite expectation $\mathbb{E} Z$. Then ($A_N$) is satisfied as we have shown before. If we choose the $N$-stage policy $\pi = (f_0, \dots , f_{N-1})$with $f_n(x) = cx$ and $c \in [0, 1]$, i.e. we always consume a constant fraction of the wealth, then the Reward Iteration implies by induction on $N$ that
$$V_{0\pi}(x)=(N+1)\log x+N\log c+\frac{(N+1)N}{2}\left(\log(1-c)+\mathbb{E}\log Z\right).$$
Hence, $\pi^*=(f_0^*, \dots , f_{N-1}^*)$ with $f_n^*(x)=c^*x$ and $c^*=\frac{2}{N+3}$ maximizes the expected log-utility (among all linear consumption policies).

---

Maximizer, the Bellman Equation & Verification Theorem

• Definition of a maximizer: Let $v\in\mathbb{M}(E)$. A decision $f\in F_n$ is called a maximizer of $v$ at time $n$ if $\mathcal{T}_{nf}(v)=\mathcal{T}_nv$, i.e. for all $x\in E$, $f(x)$ is a maximum point of the mapping $a\mapsto L_nv(x,a)$, $a\in D_n(x).$

• The Bellman Equation
  $$\begin{array}{lll} V_N&=&g_N,\\ V_n&=&\mathcal{T}_nV_{n+1},\text{ }n=1,2,\dots,N-1. \end{array}$$

• Verification Theorem: Let $(v_n) \subset\mathbb{M}(E)$ be a solution of the Bellman equation. Then it holds:

  • $v_n\geq V_n$ for $n=0,1,\dots,N$.

  • If $f_n^*$ is a maximizer of $v_{n+1}$ for $n = 0, 1, \dots, N-1$, then $v_n = V_n$ and the policy $\pi^* = (f_0^*, f_1^*, \dots , f_{N-1}^*)$ is optimal for the $N$-stage Markov Decision Problem.

---

The Structure Assumption & Structure Theorem

• Structure Assumption ($SA_N$): There exists sets $\mathbb{M}_n\subset\mathbb{M}(E)$ and $\Delta_n\subset F_n$ such that for all $n=0,1,\dots,N-1$:

  • $g_N\in\mathbb{M}_N$

  • If $v\in\mathbb{M}_{n+1}$ then $\mathcal{T}_nv$ is well-defined and $\mathcal{T}_nv\in\mathbb{M}_n$

  • For all $v\in \mathbb{M}_{n+1}$ there exists a maximizer $f_n$ of $v$ with $f_n\in \Delta_n$

• Structure Theorem: Let ($SA_N$) be satisfied. Then it holds:

  • $V_n\in\mathbb{M}_n$ and the sequence ($V_n$) satisfies the Bellman equation, i.e. for $n=0,1,,\dots,N-1$
    $$\begin{array}{lll} V_N(x)&=&g_N(x),\nonumber\\ V_n(x)&=&\sup_{a\in D_{n}(x)}\left\{r_n(x,a)+\int V_{n+1}(x')Q_n(dx'|x,a)\right\}.\text{ }x\in E.\nonumber \end{array}$$

  • $V_n=\mathcal{T}_{n}\mathcal{T}_{n+1}\dots\mathcal{T}_{N-1}g_N$

  • For $n=0,1,\dots,N-1$ there exit maximizers $f_n$ of $V_{n+1}$ with $f_n\in\Delta_n$, and every sequence of maximizers $f_n^*$ of $V_{n+1}$ defines an optimal policy $(f_0^*, f_1^*, \dots , f_{N-1}^*)$ for the $N$-stage Markov Decision Problem

• A corollary: Let ($SA_N$) be satisfied. If $n \leq m \leq N$ then it holds:
  $$V_n(x)=\sup_{\pi}\mathbb{E}_{nx}^{\pi}\left[\sum_{k=n}^{m-1}r_k(X_k,f_k(X_k))+V_m(X_m)\right],\text{ }x\in E.$$

• Backward Induction Algorithm

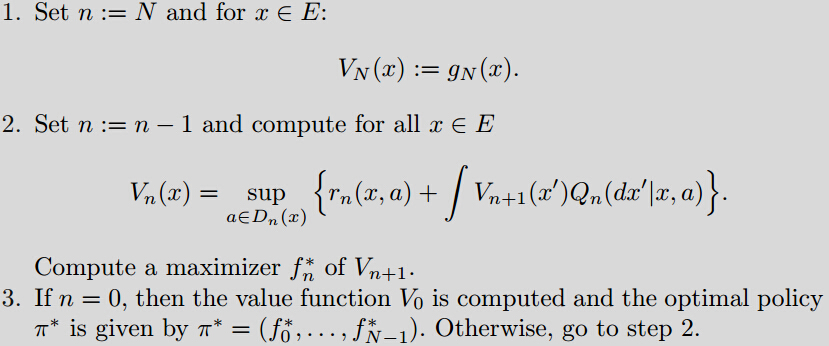
• Principle of Dynamic Programming: Let ($SA_N$) be satisfied, Then it holds for $n\leq m \leq N$:
  $$V_{n\pi^*}(x)=V_n(x)\Longrightarrow V_{m\pi^*}=V_m\text{ }\mathbb{P}_{nx}^{\pi^*}-a.s.,$$
  i.e. if $(f_n^*, \dots , f_{N-1}^*)$ is optimal for the time period $[n,N]$ then $(f_m^*, \dots , f_{N-1}^*)$ is optimal for $[m,N]$.

---

The Financial Markets

Asset Dynamics and Portfolio Strategies

Asset Dynamics and Portfolio Strategies

• We assume that asset prices are monitored in discrete time

  • time is divided into periods of length $\Delta t$ and $t_n=n\Delta t$
  • multiplicative model for asset prices: $S_{n+1}=S_n\tilde{R}_{n+1}$
  • The binomial model(\textit{Cox-Ross-Rubinstein model}) and discretization of the Black-Scholes-Merton model are two important special cases of the multiplicative model

• In what follows we will consider an N-period financial market with $d$ risky assets and one riskless bond. We assume that all random variables are defined on a probability space $(\Omega,\mathcal{F},\mathbb{P})$ with filtration ($\mathcal{F}_n$) and $\mathcal{F}_0=\{\phi,\Omega\}$.The financial market is given by:

  • A riskless bond with $S_0^0\equiv1$ and
    $$S^0_{n+1}=S^0_n(1 + i_{n+1}),\text{ }n =0, 1,\dots,N-1$$

  where $i_{n+1}$ denotes the deterministic interest rate for the time period $[n, n + 1)$. If the interest rate is constant, i.e. $i_n\equiv i$,then $S^0_n =(1+ i)^n$.

  • There are $d$ risky assets and the price process of asset $k$ is given by $S^k_0 = s^k_0$ and
    $$S^k_{n+1} = S^k_n\tilde{R}^k_{n+1},\text{ }n =0, 1,\dots,N-1$$.

  The processes ($S^k_n$) are assumed to be adapted with respect to the filtration ($\mathcal{F}_n$) for all $k$. Moreover, we suppose that $\tilde{R}^k_{n+1} > 0 \mathbb{P}-a.s.$ for all $k$ and $n$ and that $s^k_0$ is deterministic. $\tilde{R}^k_{n+1}$ is the relative price change in the time interval $[n, n + 1)$ for the risky asset $k$.

• A portfolio or a trading strategy is an ($\mathcal{F}_n$)-adapted stochastic process $\phi=(\phi^0_n,\phi_n)$ where $\phi^0_n\in\mathbb{R}$ and $\phi_n=(\phi_n^1,\dots,\phi_n^d)\in\mathbb{R}^d$ for
  $n =0, 1,\dots,N-1$. The quantity $\phi_n^k$ denotes the amount of money which is invested into asset $k$ during the time interval $[n, n +1)$.

• The vector $(\phi^0_n,\phi_n)$ is called the initial portfolio of the investor. The value of the initial portfolio is given by
  $$X_0=\sum_{k=0}^d\phi^k_0=\phi_0^0+\phi_0\cdot e$$
  %
  where $x\cdot y = \sum_{k=1}^dx_ky_k$ denotes the inner product of the vectors $x, y \in\mathbb{R}^d$ and $e=(1,\dots, 1)\in\mathbb{R}^d$.

• Let $\phi$ be a portfolio strategy and denote by $X_{n-}$ the value of the portfolio at time $n$ before trading. Then
  $$X_n= X_{n-}=\sum_{k=0}^d\phi^k_{n-1}\tilde{R}_n^k=\phi^0_{n-1}(1+i_n)+\phi_{n-1}\cdot\tilde{R}_{n}$$

• The value of the portfolio at time $n$ after trading is given by
  $$X_{n+}=\sum_{k=0}^d\phi^k_{n}=\phi^0_{n}+\phi_{n}\cdot e$$

• **Self-financing:} A portfolio strategy $\phi$ is called self-financing if
  $$X^{\phi}_{n-} = X^{\phi}_{n+}\text{ }\mathbb{P}-a.s.$$

for all $n =1,\dots,N-1$, i.e. the current wealth is just reassigned to the assets.

• Arbitrage opportunity: An arbitrage opportunity is a self-financing portfolio strategy $\phi=(\phi_n^0,\phi_n)$ with the following property: $X^{\phi}_0=0$ and
  $$\mathbb{P}(X^{\phi}_N\geq0)=1\text{ and }\mathbb{P}(X^{\phi}_N>0)>0.$$

• A theorem: Consider an $N$-period financial market. The following two statements are equivalent:

  • There are no arbitrage opportunities.
  • For $n =0, 1,\dots,N-1$ and for all $\mathcal{F}_n$-measurable $\phi_n\in\mathbb{R}^d$ it holds:
    $$\phi_n\cdot\tilde{R}_{n+1}\geq0\text{ }\mathbb{P}-a.s.\text{ }\Longrightarrow\text{ }\phi_n\cdot\tilde{R}_{n+1} =0\text{ }\mathbb{P}-a.s.$$

---

Modeling and Solution Approaches with MDP

Modeling and Solution Approaches with MDP

• Modeling approach: specify the elements of the MDP

  • state space $E$, action space $A$
  • transition function: $x_{n+1}=T_n(x_n, a_n, Z_n)$
  • value function $V_n(x_n)=\sup_{a_n,\dots,a_{N-1}}\left\{\sum_{k=n}^{N-1}g_k(x_k)+g_N(x_N)\right\}$
  • the Bellman equation: $V_n(x_n)=\sup_{a_n}\left\{g_n(x_n,a_n)+V_{n+1}(x_n,a_n,Z_n)\right\}$

• Solution approaches

  • backward induction (with the Bellman equation)
  • the existence and form of optimal policy
  • we are interested in the structured properties that are preserved in the iterations

---

MDP Applications in Finance

A Cash Balance Problem

A Cash Balance Problem

The cash balance problem involves the decision about the optimal cash level of a firm over a finite number of periods. The aim is to use the firm’s liquid assets efficiently. There is a random stochastic change in the cash reserve each period (which can be both positive and negative). Since the firm does not earn interest from the cash position, there are holding cost or \textit{opportunity cost} for the cash reserve if it is positive. But also in case the cash reserve is negative the firm incurs an out-of-pocket expense and has to pay interest. The cash reserve can be increased or decreased by the management at the beginning of each period which implies transfer costs. To keep the example simple we assume that the random changes in the cash flow are given by independent and identically distributed random variables ($Z_n$) with finite expectation. The transfer cost are linear. More precisely, let us define a function $c:\mathbb{R}\rightarrow\mathbb{R}_+$ by
$$c(z)=c_uz^++c_dz^-$$
where $c_u,c_d > 0$. The transfer cost are then given by $c(z)$ if the amount $z$ is transferred. The cost $L(x)$ have to be paid at the beginning of a period for cash level $x$. We assume that

• $L:\mathbb{R}\rightarrow\mathbb{R}_+$, $L(0)=0$,
• $L\mapsto L(x)$ is convex
• $\lim_{|x|\rightarrow\infty}\frac{L(x)}{|x|}=\infty$

Problem Formulation

• Elements of MDP

  • $E = \mathbb{R}$ where $x\in E$ denotes the cash level,
  • $A = \mathbb{R}$ where $a\in A$ denotes the new cash level after transfer,
  • $D(x)= A$,
  • $Z = \mathbb{R}$ where $z\in Z$ denotes the cash change,
  • $Q^Z(\cdot|x, a) = \text{distribution of }Z_{n+1}\text{ (independent of }(x, a)\text{)}$,
  • $r(x, a)= -c(a-x)-L(a)$,
  • $g \equiv 0$,
  • $\beta\in(0, 1]$

• The state transition function: $$x_{k+1}=T (x_k, a_k, z_k)= a_k-z_k,\text{ for }k=1,\dots,N$$

• The value function
  $$v_{n}(x_n)=\sup_{\left\{a_i\in\mathbb{R}:i=1,\dots,N\right\}}\mathbb{E}^{Z}\left[\sum_{k=n}^N\left\{\left[-c(a_n-x_n)-L(a_n)\right]+g\right\}\right],\text{ for }k=1,\dots,N$$

• The Bellman equation
  $$V_n(x_n)=\sup_{a_n\in\mathbb{R}}\mathbb{E}^{Z}\left[-c(a_n-x_n)-L(a_n)+V_{n+1}(a_n-Z_n)\right],\text{ for }k=1,\dots,N$$

---

Solution

• Solution is worked through by backward induction

• We verified the validity of Integrability Assumption ($A_N$) and the relative Structure Assumption ($SA_N$) for each $V_n(x_n)$

• The solution to the cash balance problem (Theorem 2.6.2):

  • There exist critical levels $S_{n-}$ and $S_{n+}$ such that for $n =1,\dots,N$
    $$J_n(x)=\left\{\begin{array}{cl} (S_{n-}-x)c_u+L(S_{n-})+\beta\mathbb{E}J_{n-1}(S_{n-}-Z)&\text{ if }x<S_{n-}\\ L(x)+\beta\mathbb{E}J_{n-1}(x-Z)&\text{ if }S_{n-}\leq x\leq S_{n+}\\ (x-S_{n+})c_d+L(S_{n+})+\beta\mathbb{E}J_{n-1}(S_{n+}-Z)&\text{ if }x>S_{n+} \end{array}\right.\nonumber$$

  with $J_0\equiv0$.

  • There exist critical levels $S_{n-}$ and $S_{n+}$ such that for $n =1,\dots,N$
    $$f^*_n(x)=\left\{\begin{array}{ll} S_{n-}&\text{ if }x<S_{n-}\\ x&\text{ if }S_{n-}\leq x\leq S_{n+}\\ S_{n+}&\text{ if }x>S_{n+} \end{array}\right.\nonumber$$

---

Consumption and Investment Problems

Consumption and Investment Problems

We consider now the following extension of the consumption problem of Example 2.1.4. Our investor has an initial wealth $x> 0$ and at the beginning of each of $N$ periods she can decide how much of the wealth she consumes and how much she invests into the financial market given as in Section 4.2. In particular $\mathcal{F}_n=\mathcal{F}^S_n$. The amount $c_n$ which is consumed at time $n$ is evaluated by a utility function $U_c(c_n)$. The remaining wealth is invested in the risky assets and the riskless bond, and the terminal wealth $X_N$ yields another utility $U_p(X_N)$. How should the agent consume and invest in order to maximize the sum of her expected utilities?

---

Formulation

• Assumption (FM)

  • There is no arbitrage opportunity.
  • $\mathbb{E}\|R_n\|<\infty$ for all $n=1,\dots,N$.

• As in Section 4.2 we impose the Assumption (FM) on the financial market. Moreover, we assume that the utility functions $U_c$ and $U_p$ satisfy $dom\ U_c =dom\ U_p = [0,\infty)$. Analogously to (3.1) the wealth process ($X_n$)evolves as follows
  $$X_n =(1+ i_n )(X_n-c_n + \phi n\cdot R_n )$$
  where $(c,\phi)=(c_n,\phi_n)$ is a consumption-investment strategy, i.e. ($\phi_n$)and ($c_n$)are $\mathcal{F}_n$-adapted and $0\leq c_n\leq X_n$. The consumption-investment problem is then given by
  $$\left\{\begin{array}{l} \mathbb{E}_x\left[\sum_{=0}^{N-1}U_c(c_n)+U_p(X_N^{c,\phi})\right]\rightarrow\max\\ (c,\phi)\text{ is a consumption-investment strategy with }X_N^{c,\phi}\in dom\ U_p\ \mathbb{P}=a.s. \end{array}\right.\nonumber$$

• Elements of MDP

  • $E= [0,\infty)$ where $x\in E$ denotes the wealth,
  • $A= \mathbb{R}\times\mathbb{R}^d$ where $a\in \mathbb{R}^d$ is the amount of money invested in the risky assets and $c\in R$ the amount which is consumed,
  • $D_n(x)$ is given by
    $$Dn(x)=\left\{(c,a)\in A: 0\leq c\leq x\text{ and }\right.\nonumber\\ \left.(1+i_{n+1})(x-c+a\cdot R_{n+1})\in E\text{ }\mathbb{P}-a.s.\right\}\nonumber$$
  • $X=[-1,\infty]^d$ where $z\in Z$ denotes the relative risk
  • $T_n(x,c,a,z)=(1+i_{n+1})(x-c+a\cdot z)$
  • $Q^Z_n(\cdot|x, c, a)=\text{distribution of }R_{n+1}\text{ (independent of }(x, c, a)\text{)}$,
  • $r_n(x, c, a)=U_c(c)$
  • $g_N(x)= U_p(x)$.

• The value function
  $$V_n(x)=\sup_{\pi}\mathbb{E}^{\pi}_{nx}\left[\sum_{k=n}^{N-1}U_c(c_k(X_k))+U_p(X_N)\right]$$

---

Solution

• Let $U_c$ and $U_p$ be utility functions with $dom\ U_c = dom\ U_p =[0,\infty)$. Then it holds:

  • There are no arbitrage opportunities if and only if there exists a measurable function $f^*: dom\ U_p\rightarrow A$ such that
    $$u(x,f^*(x))=v(x,\ x\in dom\ U_p)$$
  • $v(x)$ is strictly increasing, strictly concave and continuous on $dom\ U_p$.

• For the multiperiod consumption-investment problem it holds:

  • The value functions $V_n$ are strictly increasing, strictly concave and continuous.
  • The value functions can be computed recursively by the Bellman equation
    $$\begin{array}{lll} &&V_N(x)=U_p(x),\nonumber\\ &&V_n(x)=\sup_{(c,a)\in D_n(x)}\left\{U_c(c)+\mathbb{E}V_{n+1}\left((1+i_{n+1})(x-c+a\cdot R_{n+1})\right)\right\} \end{array}$$
  • There exist maximizers $f^*_n$ of $V_n$ and the strategy $(f^*_0,f^*_1,\dots,f^*_{N-1})$ is optimal for the $N$-stage consumption-investment problem.

---

Terminal Wealth Problems

Terminal Wealth Problems

Suppose we have an investor with utility function $U : dom\ U \rightarrow \mathbb{R}$ with $dom\ U =[0,\infty)$ or $dom\ U =(0,\infty)$ and initial wealth $x>0$. A financial market with $d$ risky assets and one riskless bond is given (for a detailed description see Section 3.1). Here we assume that the random vectors $R_1,\dots,R_N$ are independent but not necessarily identically distributed. Moreover we assume that $(\mathcal{F}_n)$ is the filtration generated by the stock prices, i.e. $\mathcal{F}_n = \mathcal{F}^S_n$. We make the (FM) assumption for the financial market.

Our agent has to invest all the money into this market and is allowed to rearrange her portfolio over $N$ stages. The aim is to maximize the expected utility of her terminal wealth.

---

Formulation

• The wealth process ($X_n$) evolves as follows
  $$X_{n+1}=(1+i_{n+1})(X_n+\phi_n\cdot R_{n+1})$$
  where $\phi=(\phi_n)$ is a portfolio strategy. The optimization problem is then
  $$\left\{\begin{array}{l} \mathbb{E}_xU(X^{\phi}_N)\rightarrow\max\\ \phi\text{ is a portfolio strategy and }X^{\phi}_N\in dom\ U\text{ }\mathbb{P}-a.s. \end{array}\right.\nonumber$$

• Elements of the MDP

  • $E= dom\ U$ where $x$ denotes the wealth,
  • $A= \mathbb{R}^d$ where $a$ is the amount of money invested in the risky assets,
  • $D_n(x)=\left\{a\in\mathbb{R}^d:(1+i_{n+1})(x+a\cdot R_{n+1})\in dom\ U\text{ }\mathbb{P}-a.s.\right\}$,
  • $Z= [-1,\infty)^d$ where $z$ denotes the relative risk,
  • $T_n(x, a, z)=(1+i_{n+1})(x+a\cdot z)$,
  • $Q^Z_n(\cdot|x, a)= \text{distribution of }R_n\text{ (independent of }(x, a)\text{)}$,
  • $r_n\equiv0$, and $g_N(x)= U(x)$.

---

Solution

For the multiperiod terminal wealth problem it holds:

• The value functions $V_n$ are strictly increasing, strictly concave and continuous.

• The value functions can be computed recursively by the Bellman equation
  $$\begin{array}{lll} &&V_N(x)=U(x),\\ &&V_n(x)=\sup_{a\in D_n(x)}\mathbb{E}V_{n+1}\left((1+i_{n+1})(x+a\cdot R_{n+1})\right),\ x\in E \end{array}$$

• There exist maximizers $f^*_n$ of $V_{n+1}$ and the strategy $(f^*_0,f^*_1,\dots,f^*_{N-1})$ is optimal for the $N$-stage terminal wealth problem.

---

Portfolio Selection with Transaction Costs

Portfolio Selection with Transaction Costs

We consider now the utility maximization problem of Section 4.2 (Terminal Wealth Problems) under proportional transaction costs. For the sake of simplicity we restrict to one bond and one risky asset. If an additional amount of $a$ (positive or negative) is invested in the stock, then proportional transaction costs of $c|a|$ are incurred which are paid from the bond position. We assume that $0\leq c< 1$. In order to compute the transaction costs, not only is the total wealth interesting, but also the allocation between stock and bond matters. Thus, in contrast to the portfolio optimization problems so far, the state space of the Markov Decision Model is two-dimensional and consists of the amounts held in the bond and in the stock.

---

Formulation

• Elements of the MDP

  • $E= \mathbb{E}^2_+$ where $x=(x_0,x_1)\in E$ denotes the amount invested in bond and stock,
  • $A= \mathbb{R}^2$ where $a=(a_0,a_1)\in A$ denotes the amount invested in bond and stock after transaction,
  • $D(x_0,x_1)=\left\{(a_0,a_1)\in A:a_0+a_1\leq x_0+x_1-c|a_1-x_1|\right\}$,
  • $Z= \mathbb{R}_+$ where $z\in Z$ denotes the relative price change of the stock,
  • $T_n(x, (a_0,a_1), z_{n+1})=\left(a_0(1+i_{n+1}),a_1z_{n+1}\right)$,
  • $Q^Z_n(\cdot|x, a_0, a_1)= \text{distribution of }\tilde{R}_{n+1}\text{ (independent of }(x, a_0, a_1)\text{)}$,
  • $r_n\equiv0$,
  • $g_N(x)= U(x_0+x_1),\ x=(x_0,x_1)\in E$.

---

Dynamic Mean-Variance Problems

Dynamic Mean-Variance Problems

An alternative approach towards finding an optimal investment strategy was introduced by Markowitz in 1952 and indeed a little bit earlier by de Finetti. In contrast to utility functions the idea is now to measure the risk by the portfolio variance and incorporate this measure as follows: Among all portfolios which yield at least a certain expected return (benchmark), choose the one with smallest portfolio variance. The single-period problem was solved in the 1950s. It still has great importance in real-life applications and is widely applied in risk management departments of banks. The problem of multiperiod portfolio-selection was proposed in the late 1960s and early 1970s and has been solved recently. The difficulty here is that the original formulation of the problem involves a side constraint. However, this problem can be transformed into one without constraint by the Lagrange multiplier technique. Then we solve this stochastic Lagrange problem by a suitable Markov Decision Model.
We use the same non-stationary financial market as in Section 4.2 (Terminal Wealth Problems) with independent relative risk variables. Our investor has initial wealth $x_0 > 0$. This wealth can be invested into $d$ risky assets and one riskless bond. How should the agent invest over $N$ periods in order to find a portfolio with minimal variance which yields at least an expected return of $\mu$?

---

Formulation

• Elements of the MDP

  • $E= \mathbb{R}$ where $x\in E$ denotes the wealth,
  • $A= \mathbb{R}^d$ where $a\in A$ is the amount of money invested in the risky assets,
  • $D_n(x)= A$,
  • $Z= [-1,\infty)^d$ where $z\in Z$ denotes the relative risk,
  • $T_n(x, a, z)=(1+ i_n )(x + a\cdot z)$,
  • $Q^Z_n (\cdot|x, a)=$ distribution of $R_{n+1}$ (independent of $(x, a)$).

• The original formulation (MV)
  $$(MV)\left\{\begin{array}{l} Var^{\pi}_{x_0}[X_N]\rightarrow\min\\ \mathbb{E}^{\pi}_{x_0}[X_N]\geq \mu\\ \pi\in F^N \end{array}\right.$$

• An equivalent formulation (MV$_=$)
  $$(MV_=)\left\{\begin{array}{l} Var^{\pi}_{x_0}[X_N]\rightarrow\min\\ \mathbb{E}^{\pi}_{x_0}[X_N]\geq \mu\\ \pi\in F^N \end{array}\right.$$

• Assumption (FM):

  • $\mathbb{E}\|R_n\|<\infty$ and $\mathbb{E}R_n\neq0$ for all $n =1,\dots,N$.
  • The covariance matrix of the relative risk process
    $$\left(Cov(R^j_n,R^k_n)\right)_{1\leq j,k\leq d}$$
    is positive definite for all $n =1,\dots,N$.
  • $x_0S^0_N<\mu$.

• Problem (MV) can be solved via the well-known Lagrange multiplier tecnique. Let $L_{x_0}(\pi,\lambda)$ be the Lagrange-function, i.e.
  $$L_{x_0}(\pi,\lambda)=Var^{\pi}_{x_0}[X_N]+2\lambda(\mu-\mathbb{E}^{\pi}_{x_0}[X_N])\text{ for }\pi\in F^N,\ \lambda\geq0.$$

• The Lagrange-problem for the parameter $\lambda> 0$
  $$P(\lambda)\left\{\begin{array}{l} L_{x_0}(\pi,\lambda)\rightarrow\min\\ \pi\in F^N \end{array}\right.$$

• A stochastic LQ-problem
  $$QP(b)\left\{\begin{array}{l} \mathbb{E}^{\pi}_{x_0}\left[(X_N-b)^2\right]\rightarrow\min\\ \pi\in F^N \end{array}\right.$$
  If $\pi^*$ is optimal for $P(\lambda)$,then $\pi^*$ is optimal for $QP(b)$ with $b=\mathbb{E}^{\pi^*}_{x_0}[X_N]+ \lambda$.

• Elements od MDP

  • $r_n(x,a)=0$,
  • $g_N(x)=-(x-b)^2$

• Solution
  
  
  
  

• Dynamic Mean-Risk Problems

---

Index Tracking

Index Tracking

The problem of index-tracking which is formulated below can be seen as an application of mean-variance hedging in an incomplete market. Suppose we have a financial market with one bond and d risky assets as in Section 3.1. Besides the tradeable assets there is a non-tradable asset whose price process
$(\tilde{S}_n)$ evolves according to
$$\tilde{S}_{n+1} =\tilde{S}_n\tilde{R}_{n+1}$$.
The positive random variable $\tilde{R}_{n+1}$ which is the relative price change of the non-traded asset may be correlated with $R_{n+1}$. It is assumed that the random vectors $(R_1,\tilde{R}_1),(R_2,\tilde{R}_2),\dots$ are independent and the joint distribution of $(R_n,\tilde{R}_n)$ is given. The aim now is to track the non-traded asset as closely as possible by investing into the financial market. The tracking error is measured in terms of the quadratic distance of the portfolio wealth to the price process $(\tilde{S}_n)$, i.e. the optimization problem is then
$$\left\{\begin{array}{l} \mathbb{E}_{x\tilde{S}}\left[\sum_{n=0}^N\left(X^{\phi}_n-\tilde{S}_n\right)^2\right]\rightarrow\min\\ \phi=(\phi_n)\text{ is a portfolio strategy} \end{array}\right.$$
where $\phi_n$ is $\mathcal{F}_n = \sigma(R_1,\dots,R_n,\tilde{R}_1,\dots,\tilde{R}_n)$-measurable.

---

Formulation

• Elements of the MDP

  • $E= \mathbb{R}\times\mathbb{R}$ where $(x, \tilde{s})\in E$ and $x$ is the wealth and $\tilde{s}$ the value of the non-traded asset,
  • $A=\mathbb{R}^d$ where $a\in A$ is the amount of money invested in the risky assets,
  • $D(x,\tilde{s})= A$,
  • $Z= (-1,\infty)^d\times\mathbb{R}_+$ where $z =(z_1,z_2)\in Z$ and $z_1$ is the relative risk of the traded assets and $z_2$ is the relative price change of the non-traded asset.
  • The transition function is given by
    $$T_n((x,\tilde{s}),a,(z_1,z_2))=\left(\begin{array}{cc}1+i_{n+1}&0\\0&z_2\end{array}\right)\left(\begin{array}{c}x\\\tilde{s}\end{array}\right)+\left(\begin{array}{c}(1+i_{n+1})z_1^T\\0\end{array}\right)a$$
  • $Q^Z_n(\cdot|(x,\tilde{s},a)=$ joint distribution of $(R_{n+1},\tilde{R}_{n+1})$ (independent of $((x,\tilde{s}),a)$),
  • $r_n((x,\tilde{s}),a)= -(x - \tilde{s})$
  • $g (x,\tilde{s})= -(x - \tilde{s})$.

• Value function (cost-to-go)
  $$V_n(x,\tilde{s})=\inf_{\pi}\mathbb{E}^{\pi}_{nx\tilde{s}}\left[\sum_{k=n}^N(X_k-\tilde{S}_k)^2\right]$$