正则化:岭回归与LASSO
| 方法 | 惩罚 | 典型用例 |
|---|---|---|
| 岭回归 | 收缩系数,处理多重共线性 | |
| LASSO | 特征选择 → 稀疏模型 | |
| 弹性网 | 结合两者优点 |
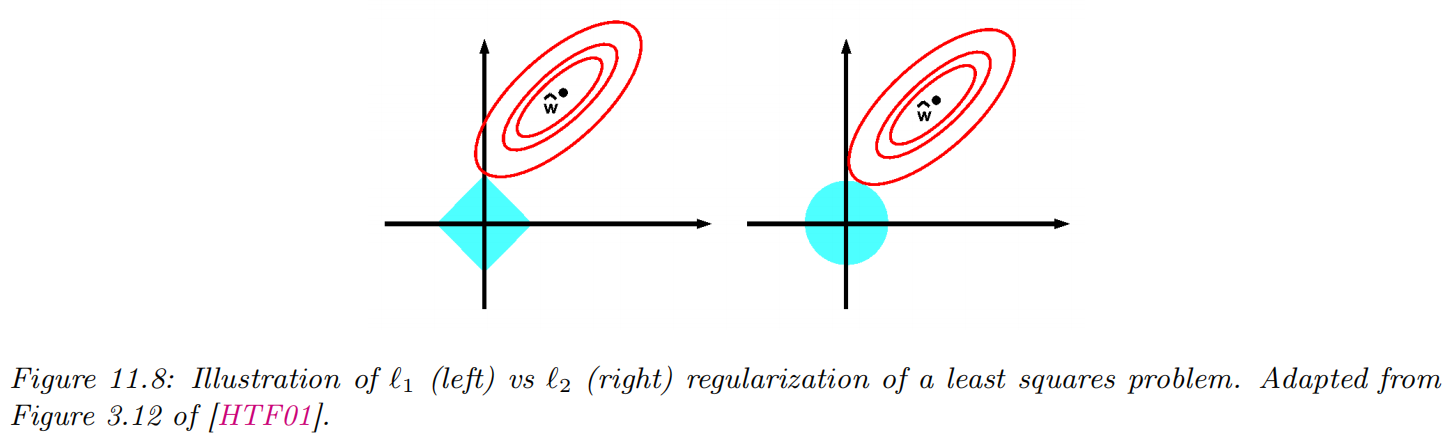
后LASSO与两步估计
- 核心思想:使用 LASSO 进行特征选择 → 仅对所选特征进行 OLS 重新拟合。
- 过程:
- 步骤 1:运行 LASSO 并定义支持集
- 步骤 2:限制在所选变量上的 OLS 估计
- 直觉:
- LASSO = 收缩 + 选择
- 后LASSO = 通过 OLS 重新拟合消除收缩偏差
- 如果支持
LASSO与后LASSO(OLS选择后)
|
实证金融应用
|
关键要点:
“使用机器学习进行选择,使用计量经济学进行估计。”
结构化正则化 · 群体 LASSO
动机:
- 在许多金融数据集中,变量是 自然分组 的(如行业部门、因子家族、宏观类别)。
- 传统的 LASSO 将每个特征单独对待,这可能会破坏结构。
- ➜ 群体 LASSO 鼓励 在组级别上稀疏。
公式
其中
关键思想:
- 如果
- 产生块稀疏解 → 选择整个经济主题或行业因子。
与标准 LASSO 的比较
|
实证金融应用
|
好处: 更高的稳定性,更好的经济解释,在分组设计中的预测改进。
岭回归 · LASSO · 弹性网特征与用例比较
| 方面 | 岭回归 | LASSO | 弹性网 |
|---|---|---|---|
| 特征选择 | 否 | 是 | 组级 |
| 处理共线性 | 强 | 可能丢弃相关变量 | 好的折中 |
| 偏差与方差 | 低方差,高偏差 | 选定变量倾向于高方差 | 平衡 |
| 参数计数 | 保留所有 | 几个非零 | 中等 |
| 可解释性 | 收缩系数 | 稀疏解释 | 组选择 |
| 金融用例 | 收益曲线, 带共线性的风险溢价 |
高维特征筛选 | 主题因子 组 |
模型训练管道
|
|
典型金融应用和关键要点
-
典型金融应用
- 横截面收益预测: LASSO / 弹性网进行因子筛选
- 收益曲线 / 期限结构: 岭回归用于强共线性
- 分组因子(价值、动量、盈利能力): 弹性网或群体 LASSO
- 信用风险建模: 弹性网用于稳定预测和可解释性
-
关键要点
- 岭回归: 保持所有变量 → 稳定性
- LASSO: 稀疏性 → 可解释性
- 弹性网: 两者的最佳结合
- 通过交叉验证选择模型 → 平衡偏差与方差
- 对于推理 → 使用 后 LASSO OLS
非线性回归:多项式回归
|
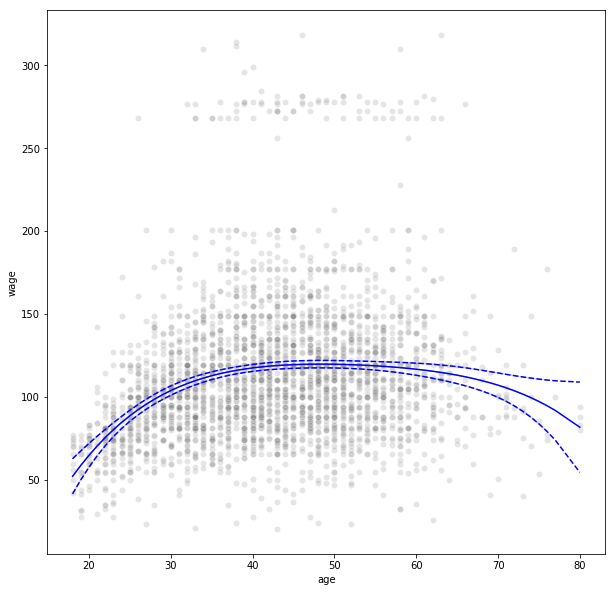
|
非线性回归:阶梯函数
|

|
非线性回归:基函数
- 多项式和分段常数回归模型是基于基函数方法的特例。
- 基函数:可以应用于变量
- 模型
- 一些基函数的示例
- 多项式函数
- 分段常数函数
- 小波
- 傅里叶级数
- 样条
非线性回归:回归样条
|
分段多项式
约束与样条
|
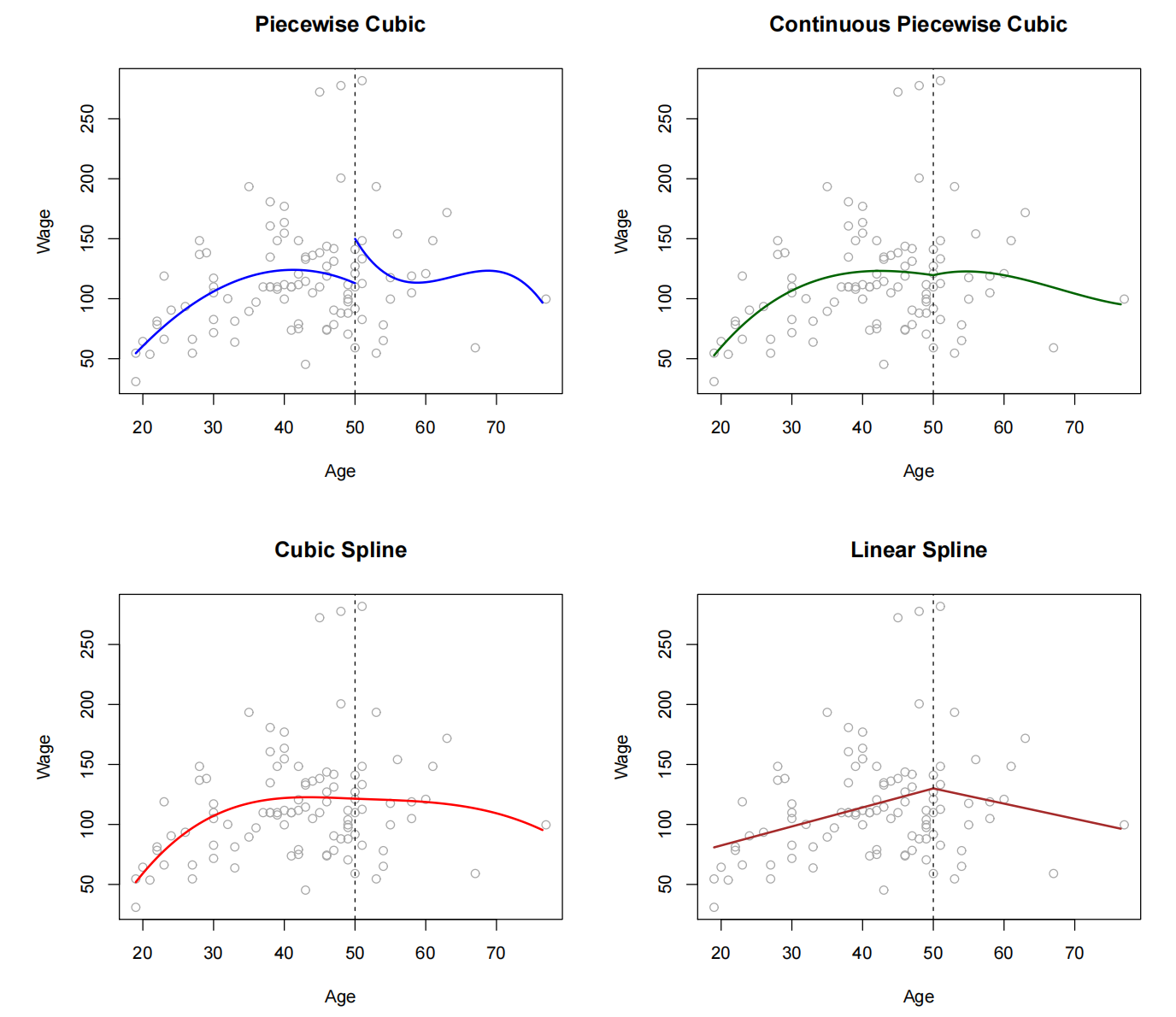
|
样条基函数表示
- 回归样条:
- 样条基
- 多项式基:
- 每个节点的截断幂基
- 多项式基:
- 样条在预测变量的外部范围可能具有高方差
- 自然样条
- 一种带有额外边界约束的回归样条
- 要求在边界处线性
- 自然样条通常在边界处产生更稳定的估计
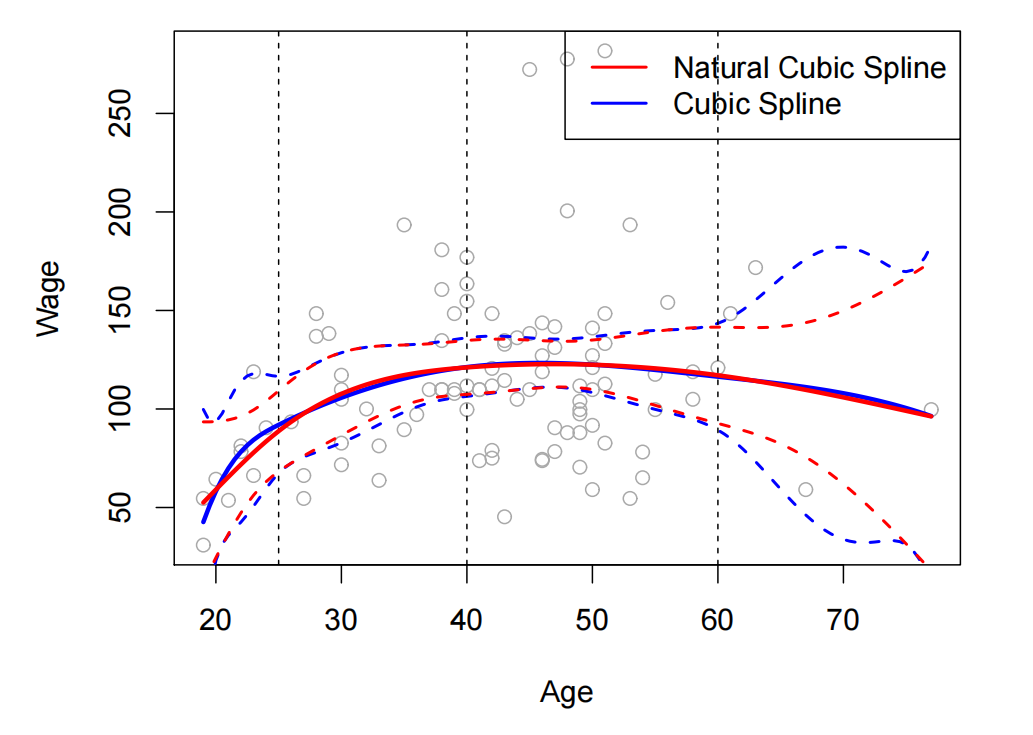
选择节点的数量与位置
|
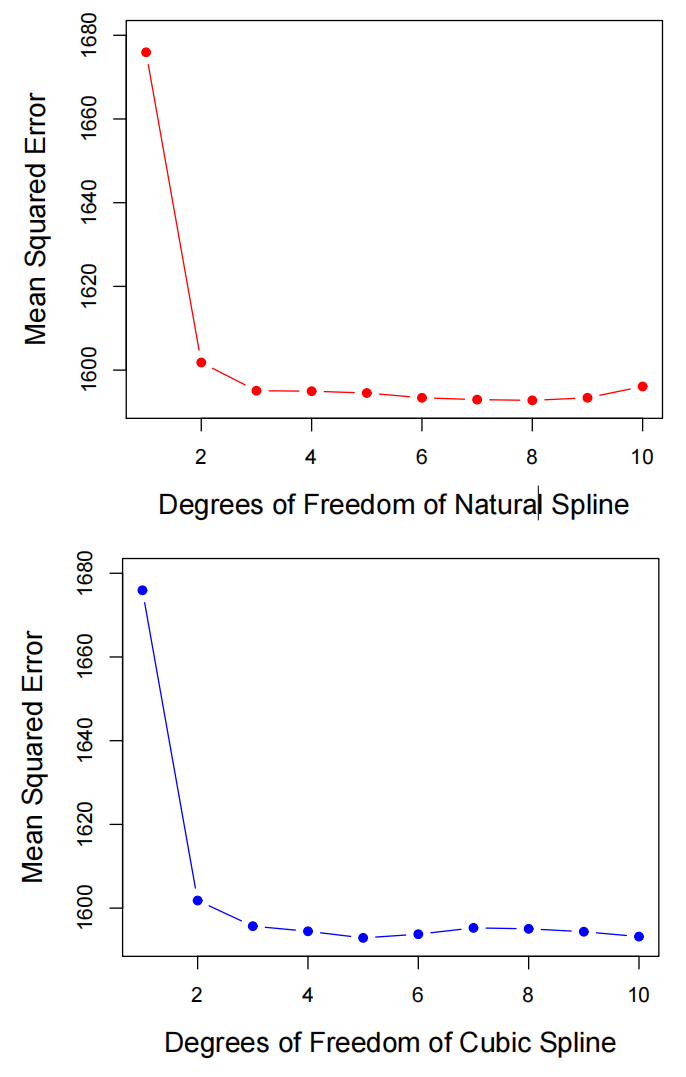
|
与多项式回归的比较
|
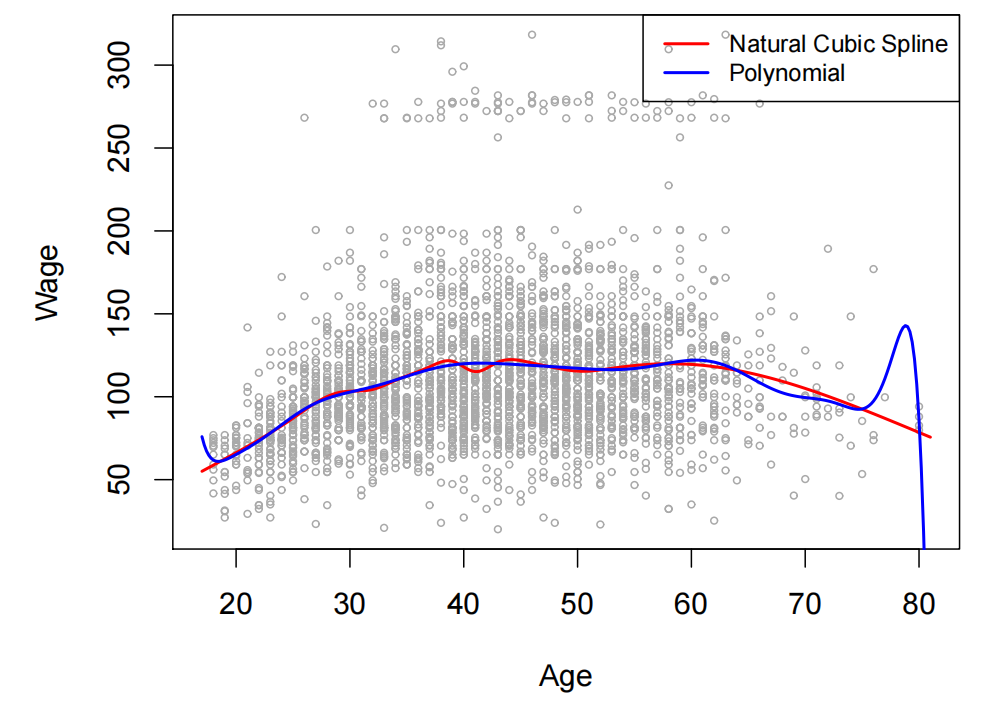
|
平滑样条
- 拟合曲线:最小化 RSS
- 平滑样条最小化以下目标
- 平滑样条是一个在
- 在
- 在每个节点处有连续的第一和第二导数
- 在极端节点外线性
- 它是这样的自然立方样条的一个缩小版本
- 在
非线性回归:局部回归
|
计算目标点 |
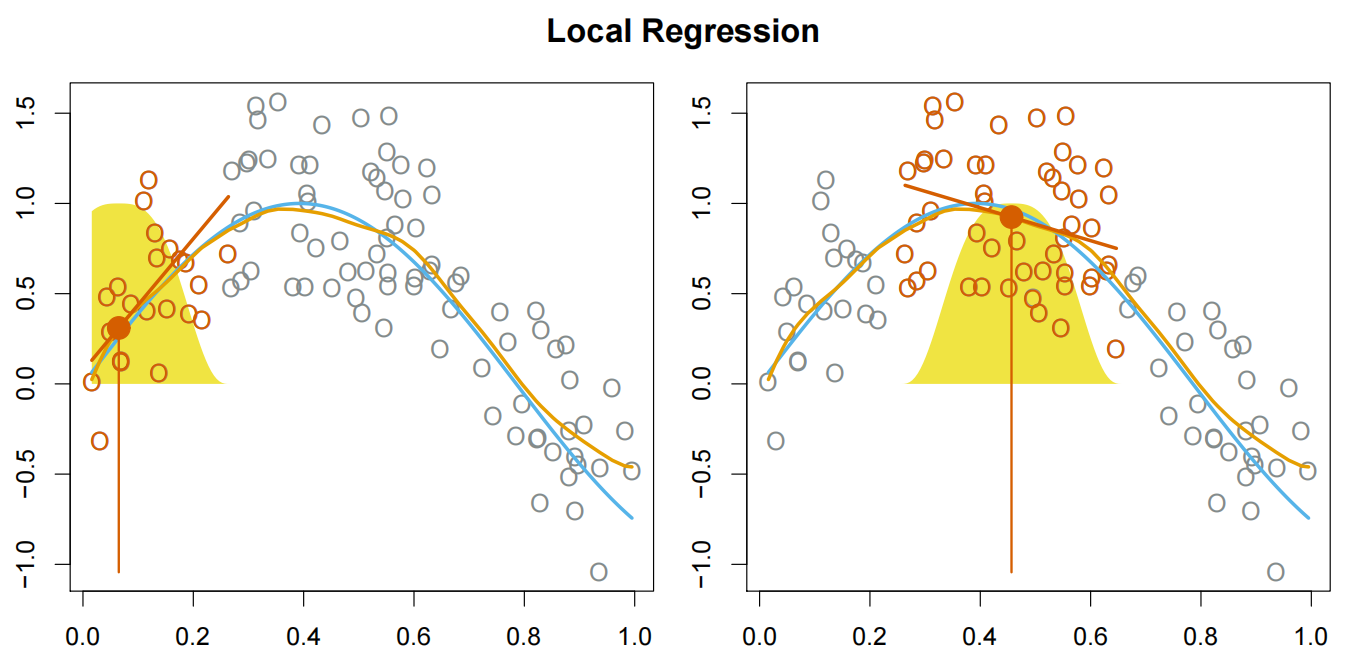
|
局部线性回归
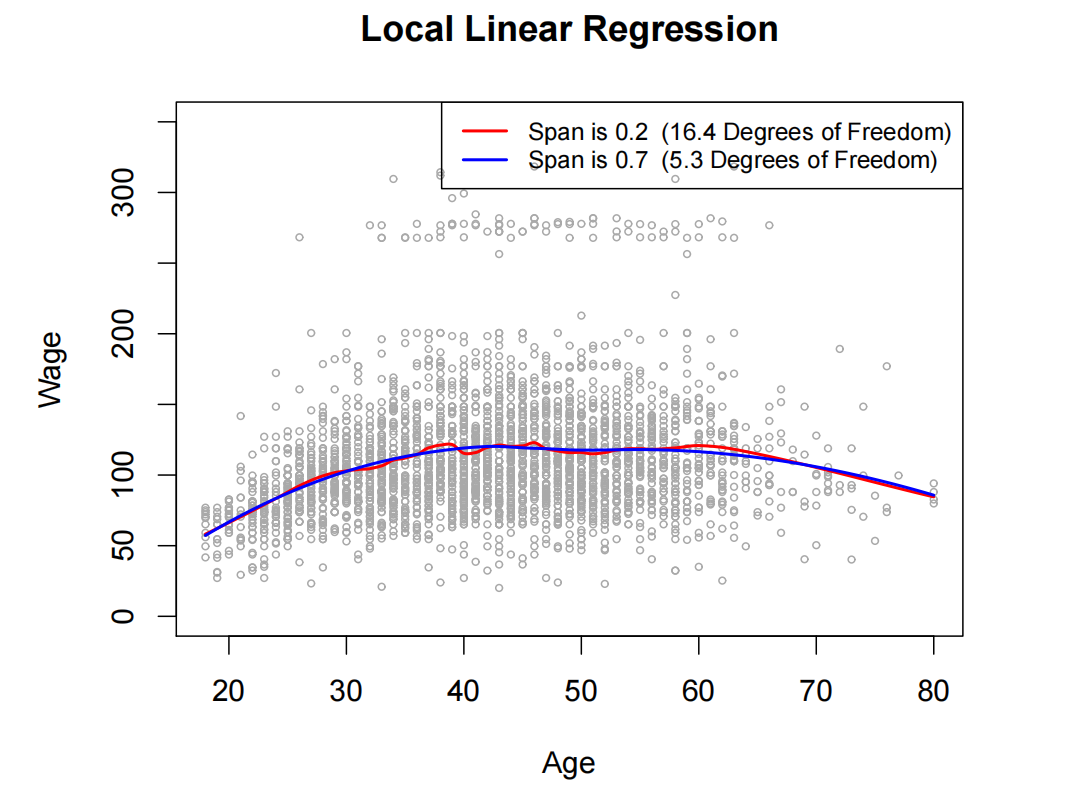
|
|
非线性回归:广义加性模型
-
多重线性回归模型
-
GAM
-
示例
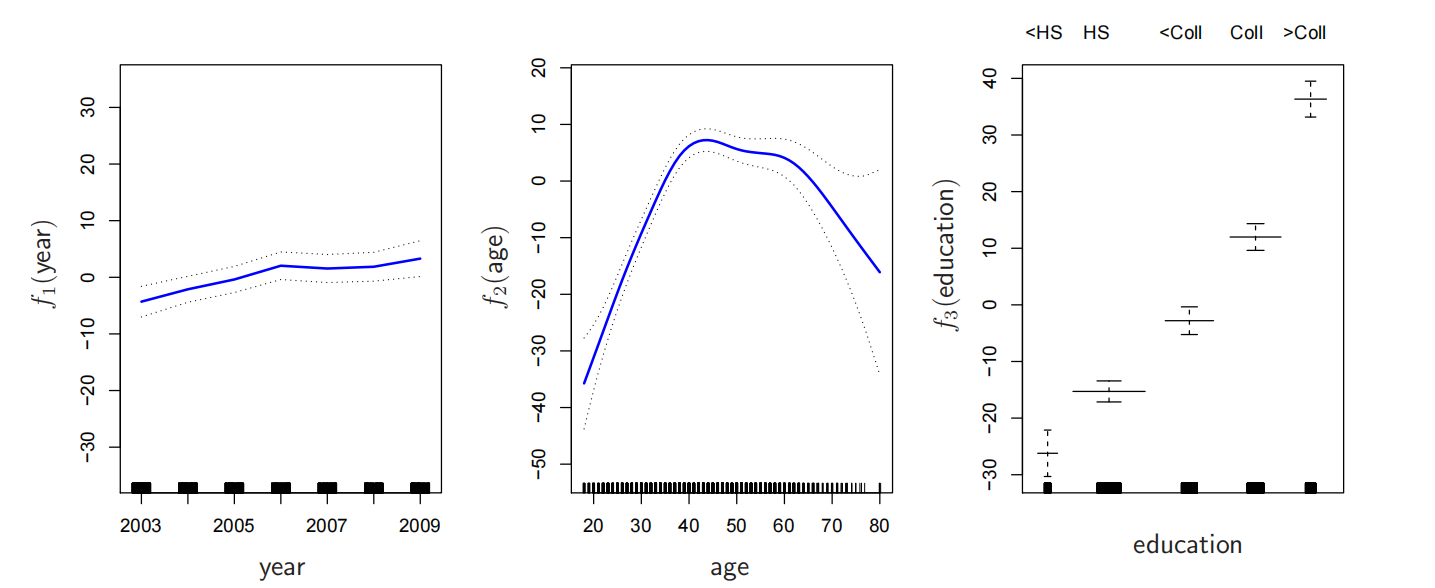
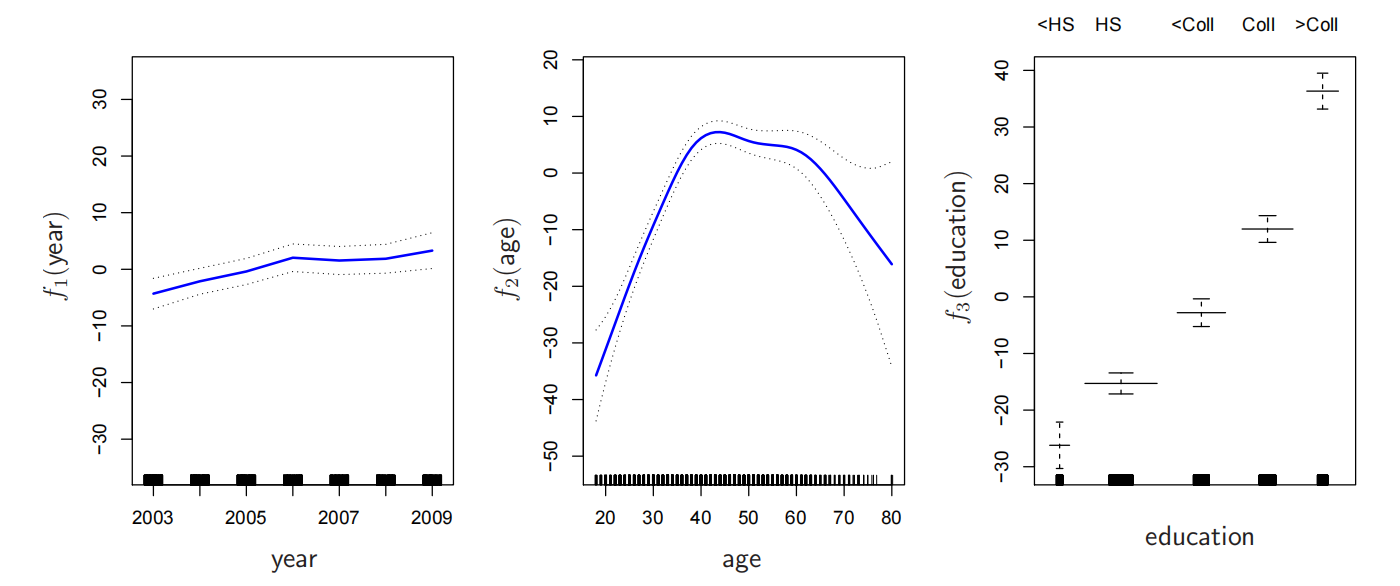
工 资 年 份 年 龄 教 育 - 年龄和年份是定量变量
- 教育是包含五个级别的定性变量:< 高中, 高中, <大学, 大学, >大学
|
自然样条 |
|
|
平滑样条 |
|
GAM 的优缺点
- 优点
-
GAM 自动建模标准线性回归会遗漏的非线性关系。
-
非线性拟合可以为响应
-
在固定其他变量的情况下,可以逐个检查每个
-
-
- 缺点:模型限制为加性。
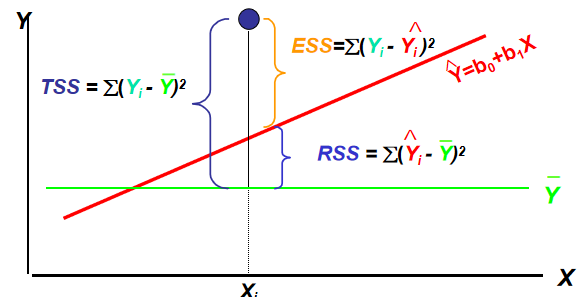
回归模型的评估
|
|
关键思想:
始终在样本外或保留集中评估以避免虚假拟合。
第 2 部分 · 分类算法
动机
- 许多金融决策是离散性的:违约/不违约、涨/跌、风险/安全。
- 需要估计分类概率与不平衡样本性能(如信用评分、欺诈检测)。
- 从 Logit 到 SVM 再到集成方法,增强金融判断的精度与可解释性。
分类作为风险与不确定性下二元决策的基础。
分类问题
-
预测离散标签
- 分类器估计
- 分类器估计
-
金融中的例子:
- 信用违约(违约/不违约)
- 欺诈检测(欺诈/不欺诈)
- 市场回报趋势(上涨/下跌)
-
回归不适合分类任务
- 回归方法不能处理超过两个类别的定性响应
- 回归方法无法提供响应的条件概率估计
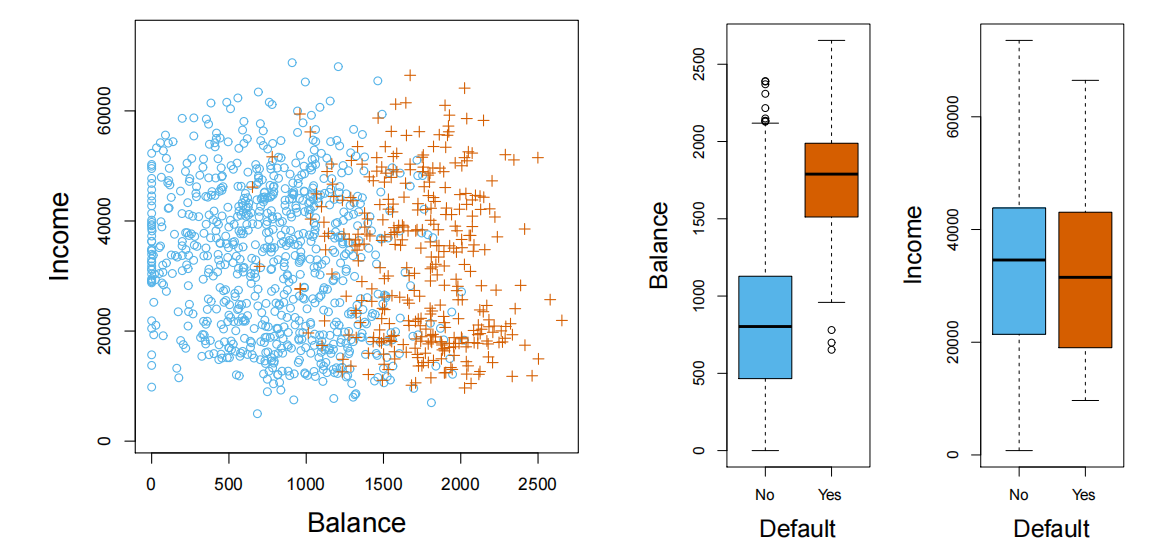
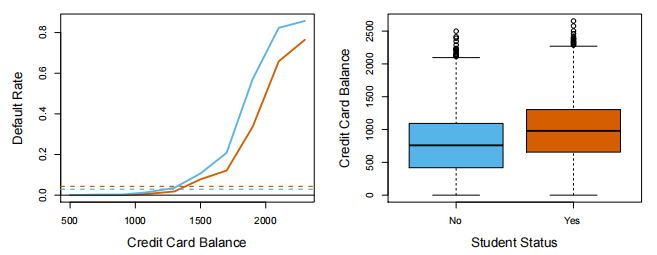
示例:违约数据集
|
|
数据来源:ISLP
逻辑模型
|
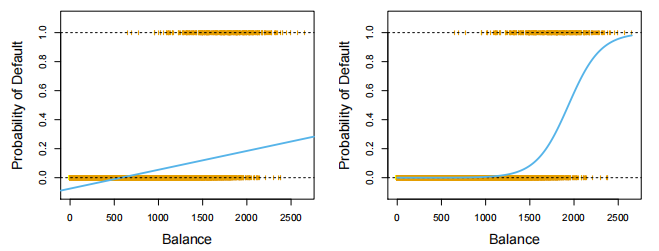
数据来源:ISLP |
多重逻辑回归
|
|
预测
|
|
多项逻辑回归
-
为具有两个以上类别的响应变量分类
-
模型
- 对于
- 对于
- 对于
- 对数赔率(对于
用于分类的生成模型
-
生成模型用于分类的核心思想
- 分别建模每个响应类别
- 使用贝叶斯定理将其转换为对
- 分别建模每个响应类别
-
为什么我们需要用于分类的生成模型
- 当两个类别之间存在显著分离时,逻辑回归模型的参数估计非常不稳定
- 如果每个类别中预测变量
- 本节中的方法可以自然地扩展到两个以上响应类别的情况
- 假设定性响应变量
- 设
- 设
- 后验 概率(贝叶斯定理)
- 估计
- 不直接计算后验概率
- 不直接计算后验概率
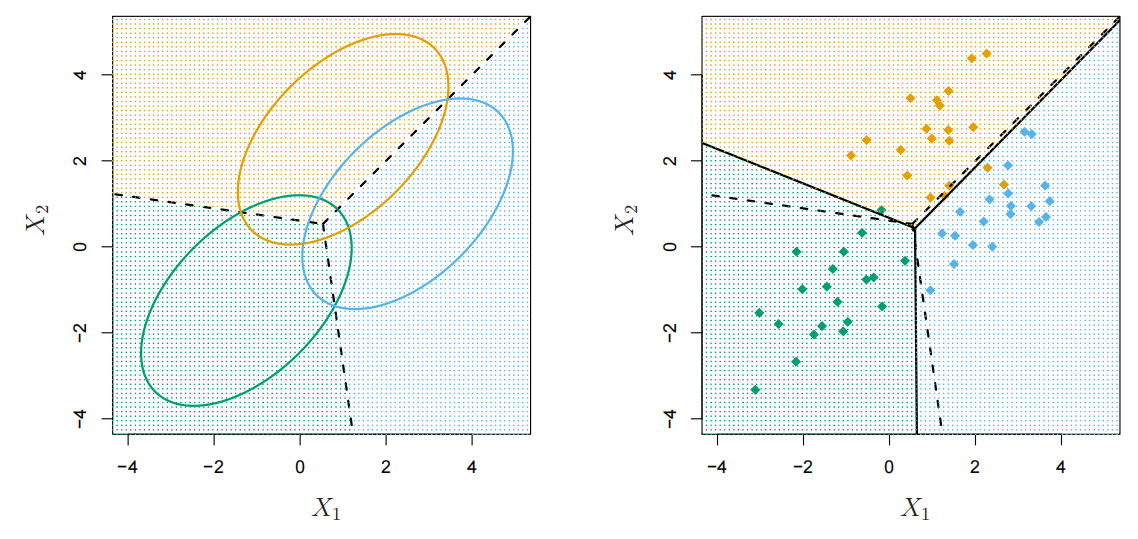
逻辑判别分析(LDA)
- 假设
- 仅有一个预测变量:
- 仅有一个预测变量:
- 后验
- 预测
- 将观察值分类为后验概率
- 等价法则:将观察值分配给最大化
- 将观察值分类为后验概率
一个示例
|
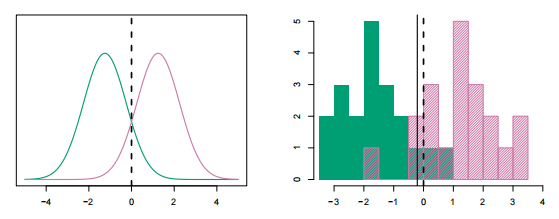
|
多维 LDA 适用于
|
多变量高斯分布 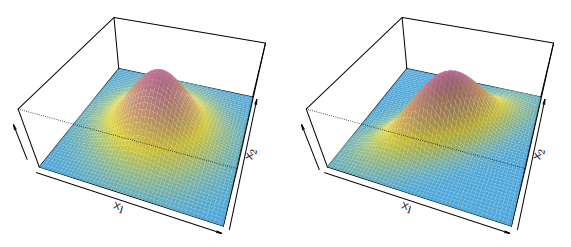
|
|
|
|
二次判别分析(QDA)
|
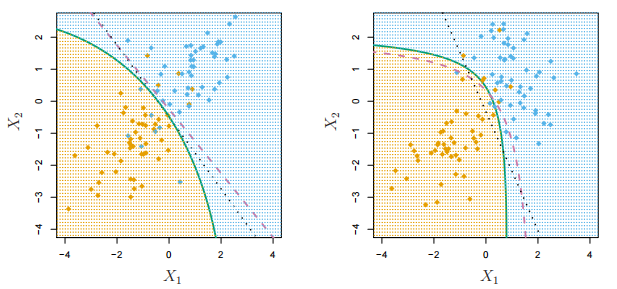
|
朴素贝叶斯
- 假设:在第
- 后验概率
- 用训练数据
- 如果
- 如果
- 为第
- 核密度估计
- 为第
- 如果
- 如果
广义加性模型
将对数赔率比建模为广义加性模型:
支持向量机
- 1990 年代开发
- 在多种环境中表现良好
- 通常被认为是最佳的“开箱即用”分类器。
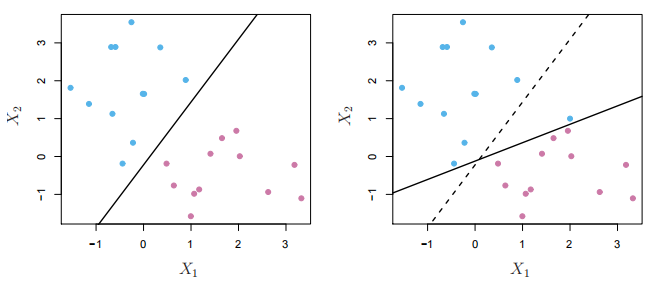
支持向量机:最大间隔分类器
|
超平面
|
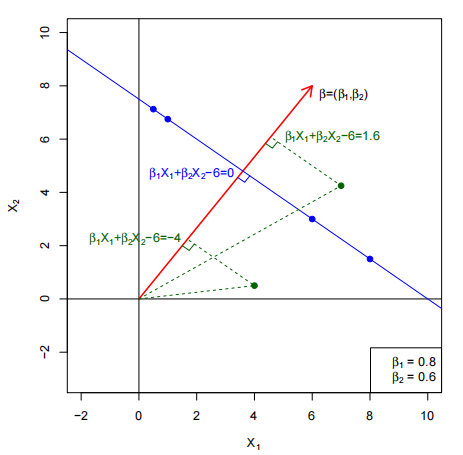
|
使用分隔超平面的分类
|
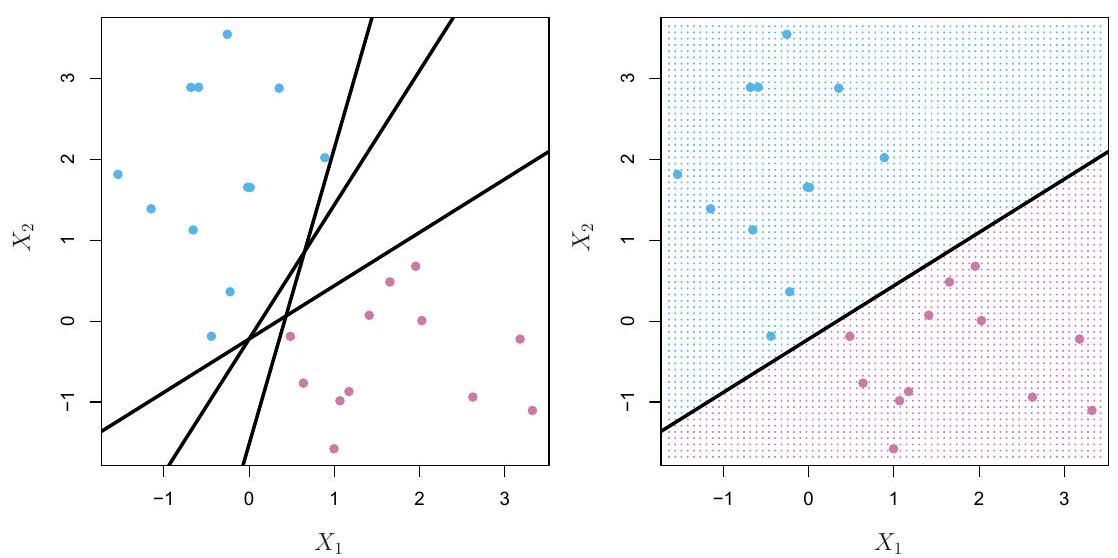
|
最大间隔分类器
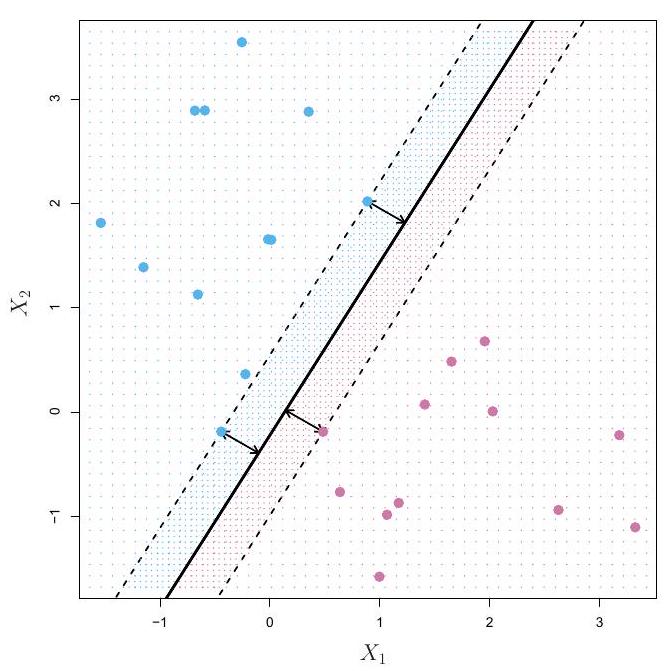
|
|
非分隔案例与噪声数据
|
|
|
|
支持向量分类器
|
|
参数
|
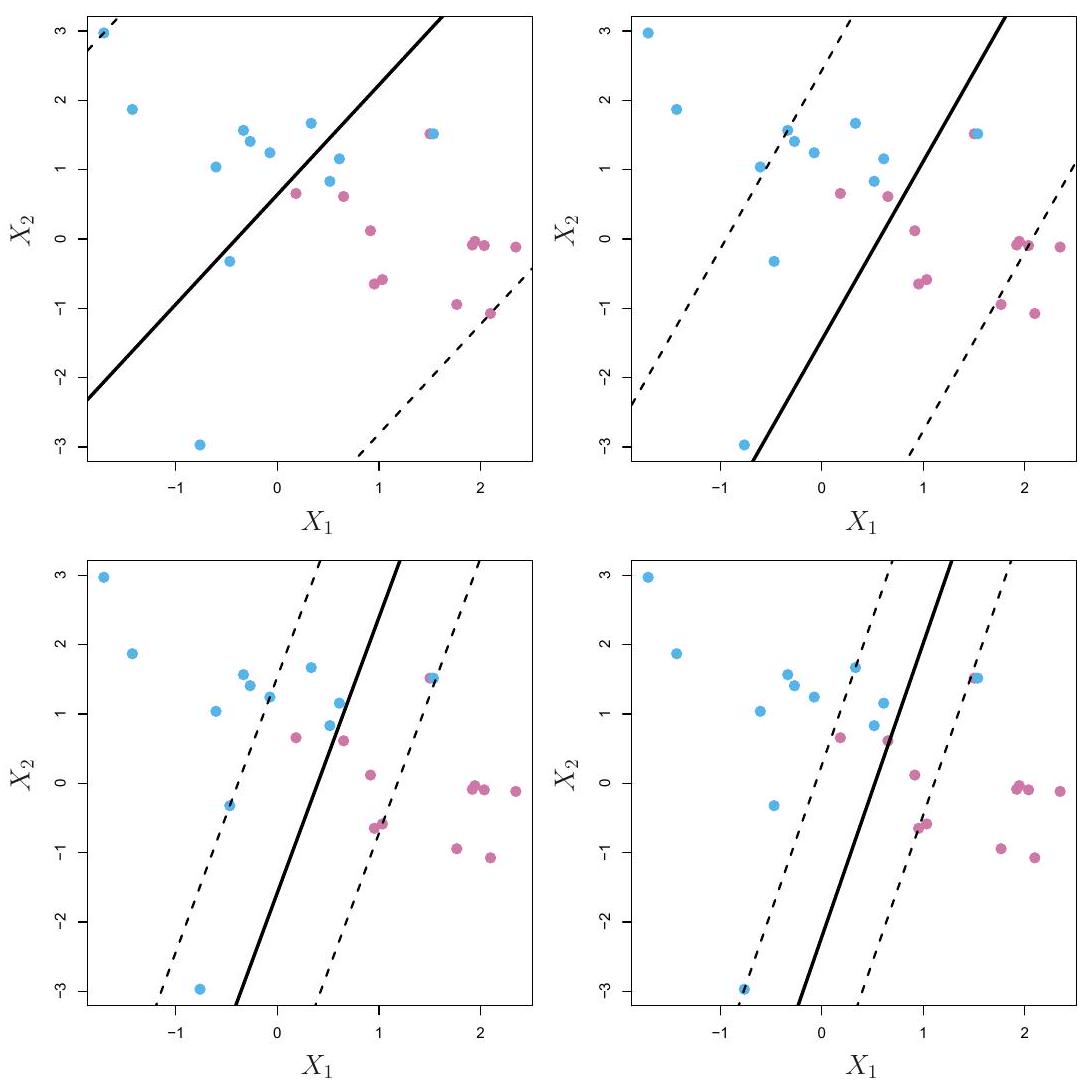
|
支持向量机
支持向量机无法处理非线性问题。
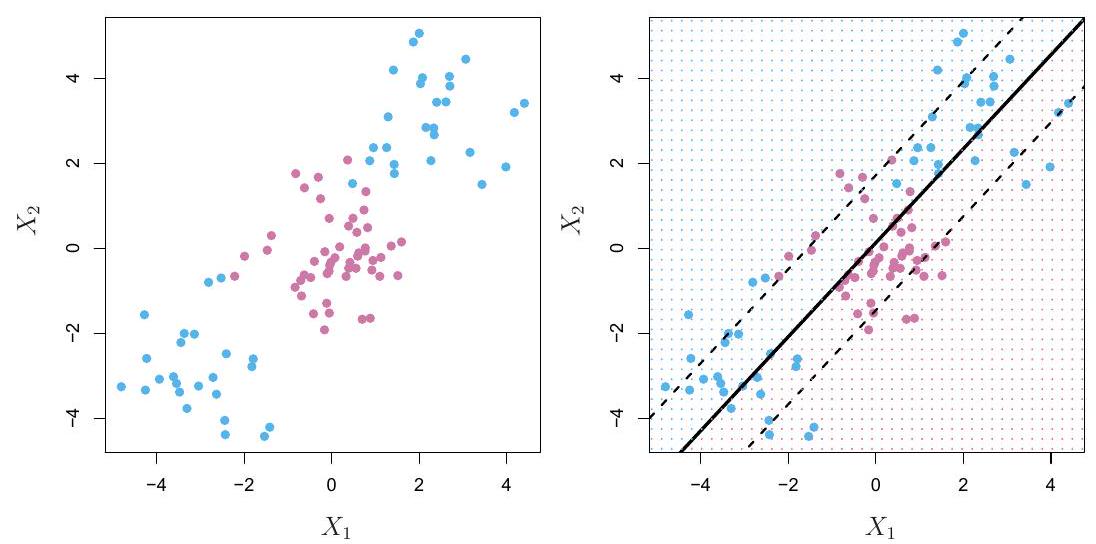
我们该怎么办?
利用多项式特征的非线性分类器
|
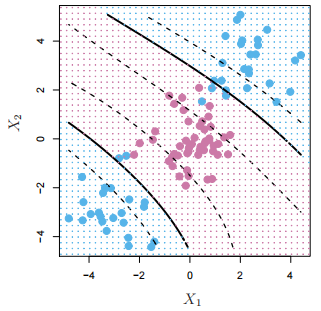
|
核函数
- 定义:
| 名称 | 函数 |
|---|---|
| 线性核 | |
| 多项式核 | |
| 径向核 | |
| 高斯核 | |
| 拉普拉斯核 | |
| Sigmoid 核 |
假设
- 对于任意函数
SVC 和 SVM
|
|
SVC
|
SVM
|
|
内积 / 核
|
|
|
|
函数形式
|
|
|
|
|
|
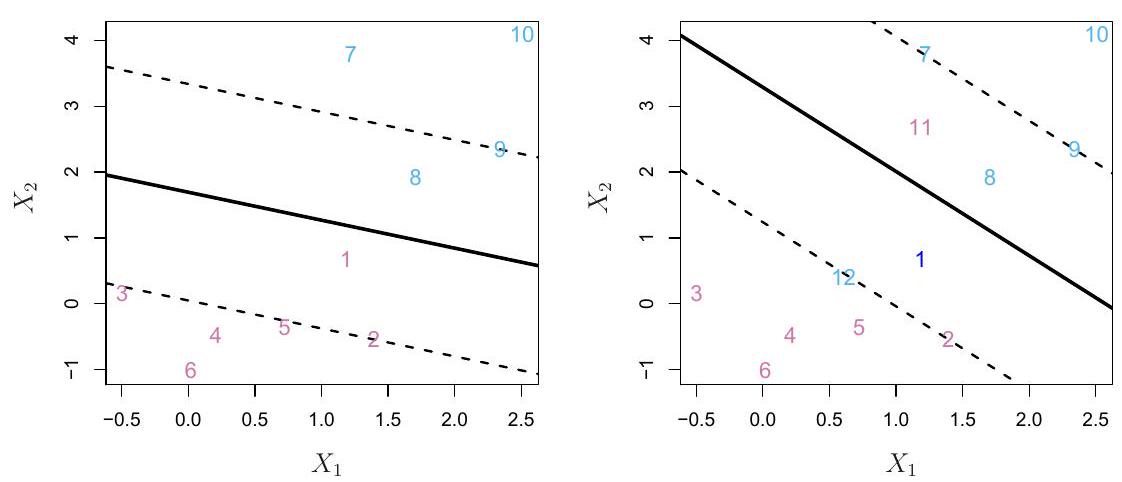
多类支持向量机
-
一对一 (OVO) 分类
- 又称全对
- 为每对类别构建一个 SVM
- 使用每个 SVM 对测试观察值进行分类
- 将观察值分配给被最频繁分配的类别
-
一对多 (OVA) 分类
- 也称一对其余
- 为每个类拟合
- 令
- 将观察值分配给
与逻辑回归的关系
- 铰链损失 + 惩罚 形式的支持向量分类器优化:
- 令
- 优化模型
- 令
- 它与逻辑回归中的“损失”(负对数似然)非常相似。
- SVM vs. 逻辑回归
- 当类(几乎)可分时,SVM 优于 LR。LDA 也是如此。
- 当不可分时,LR(带岭惩罚)与 SVM 非常相似。
- 如果需要估计概率,选择 LR。
- 对于非线性边界,核 SVM 很受欢迎。也可以在 LR 和 LDA 中使用核,但计算更为
分类模型评估
| 指标 | 目标 |
|---|---|
| 混淆矩阵 | 真/假正率和负率 |
| 准确率 | 整体分类率 |
| 精确率与召回率 (PR) | 对于不平衡数据的关键权衡 |
| ROC / AUC | 概率排名质量 |
| KS 统计量 | 信贷风险的区分能力 |
金融实践 → PD 模型评估、欺诈检出率、风险控制敏感性分析。
分类算法核心思想速览
| 方法 | 数学思想/假设 | 非线性能力 | 输出 | 主要优势 |
|---|---|---|---|---|
| 逻辑回归 | 线性决策边界;估计 |
低 | 概率 | 高度可解释、标准误可得 |
| LDA | 类条件正态且协方差相同 | 线性 | 概率 | 稳定、最小误差界 |
| QDA | 类条件正态但协方差不同 | 中高 | 概率 | 能拟合不同形状边界 |
| 朴素贝叶斯 | 特征条件独立 | 中 | 概率 | 简单、高维文本类适用 |
| GAM | 多变量非线性可加 | 高 | 概率或期望 | 灵活且可解释 |
| 支持向量机 | 最大化间隔,核函数映射 | 高 | 离散决策 | 对噪声鲁棒、边界清晰 |
经济与金融研究典型应用
| 场景 | 适用方法 | 说明 |
|---|---|---|
| 信用评分 / 违约预测 | 逻辑回归, GAM | 监管认可、可解释概率输出 |
| 企业破产 / 风险等级 | LDA, QDA | 经典统计判别思路 |
| 欺诈检测 | 支持向量机, 朴素贝叶斯 | 高维特征、复杂分类边界 |
| 市场状态识别(牛市/熊市) | 支持向量机, GAM | 可构建非线性或时变边界 |
| 文本情绪正负分类 | 朴素贝叶斯, 支持向量机 | 高维稀疏词向量场景 |
| 宏观政策立场分类 | 逻辑回归, GAM | 输出概率方便经济解释 |
模型比较
| 比较维度 | 逻辑回归 | LDA | QDA | 朴素贝叶斯 | GAM | 支持向量机 |
|---|---|---|---|---|---|---|
| 可解释性 | 高 | 高 | 中 | 中 | 高 | 低 |
| 非线性能力 | 中 | 弱 | ||||
| 小样本性能 | 可能过拟合 | 需要正则化 | 中 | |||
| 高维特征容忍度 | 需要正则化 | 不佳 | 不佳 | 依赖核 | ||
| 输出形式 | 概率 | 概率 | 概率 | 概率 | 概率/期望 | 类别或分数间隔 |
| 计算效率 | 高 | 高 | 中 | 高 | 中 | 相对较慢 |
| 监管接受度 | 中 | 中 | 低 | |||
| 典型数据结构 | 表格结构 | 连续特征 | 连续特征但方差不同 | 离散文本/分类 | 多维非线性时序 | 高维非线性 |
经济金融研究中“方法—场景”匹配表
| 任务 | 数据特点 | 推荐算法 | 原因 |
|---|---|---|---|
| 信用评分 / 违约概率 | 中小样本、易解释 | 逻辑回归或GAM | 输出概率、可视化解释、合规 |
| 企业分类 / 财务风险层级 | 多变量但正态性可近似 | LDA/QDA | 经典实证传统 |
| 文本或信件分类 | 高维词频、稀疏 | 朴素贝叶斯或支持向量机 | 对高维文本表现优 |
| 宏观经济状态判别 | 非线性、多因素 | GAM或支持向量机 | 可捕捉非线性或边界变化 |
| 市场操纵 / 欺诈检测 | 噪声多、复杂模式 | 支持向量机或GAM | 强非线性识别能力 |
总结
建议:
|
|
第 3 部分 · 基于树的模型
动机
- 捕捉数据中非线性关系与变量交互效应。
- Bagging / Boosting 等集成方法提升预测精度与鲁棒性。
- 满足金融机构对模型透明度和可解释性监管要求。
基于树的方法结合了准确性和可解释性,架起了金融中的预测与解释之间的桥梁。
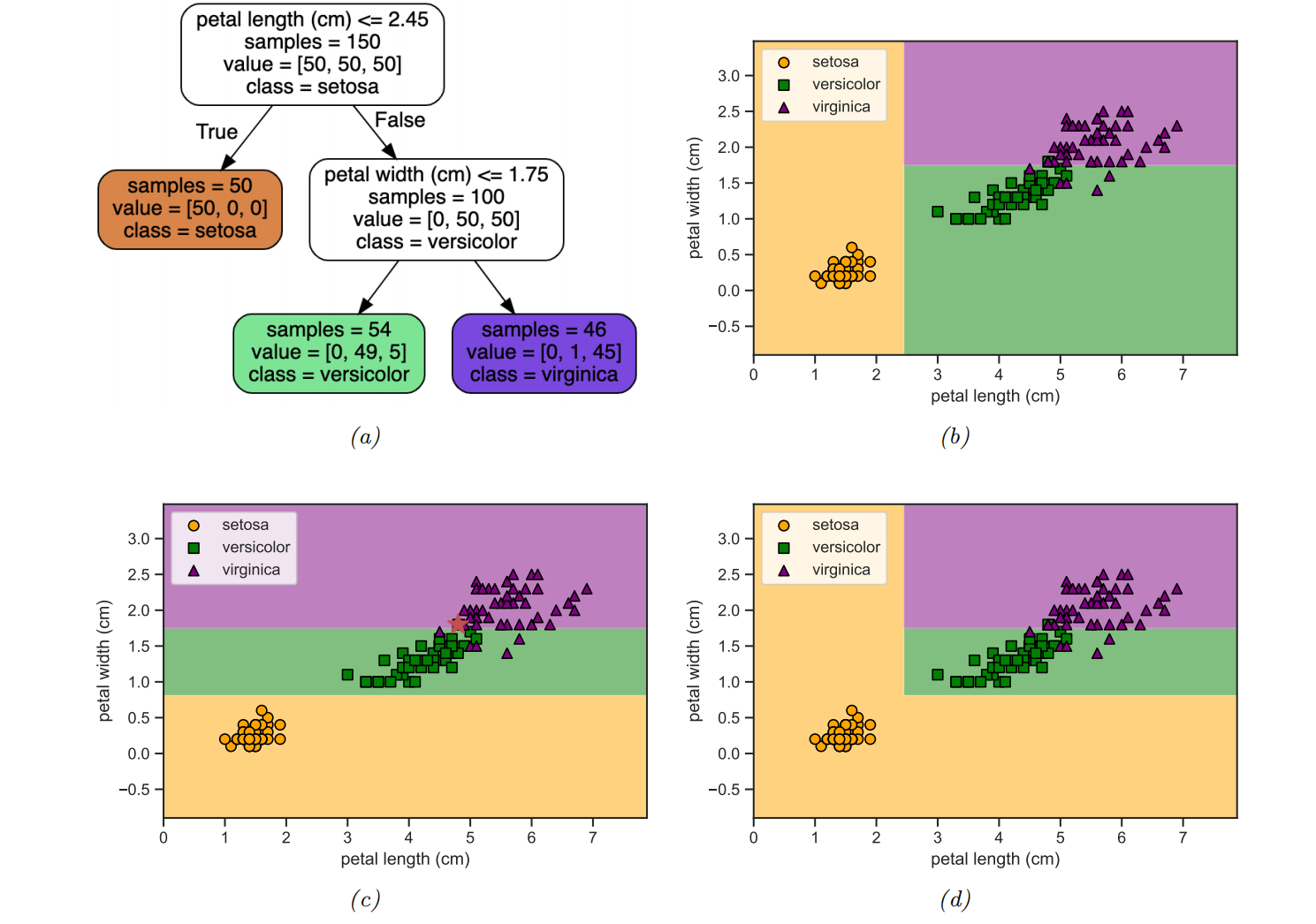
分类与回归树 (CART):回归树
|
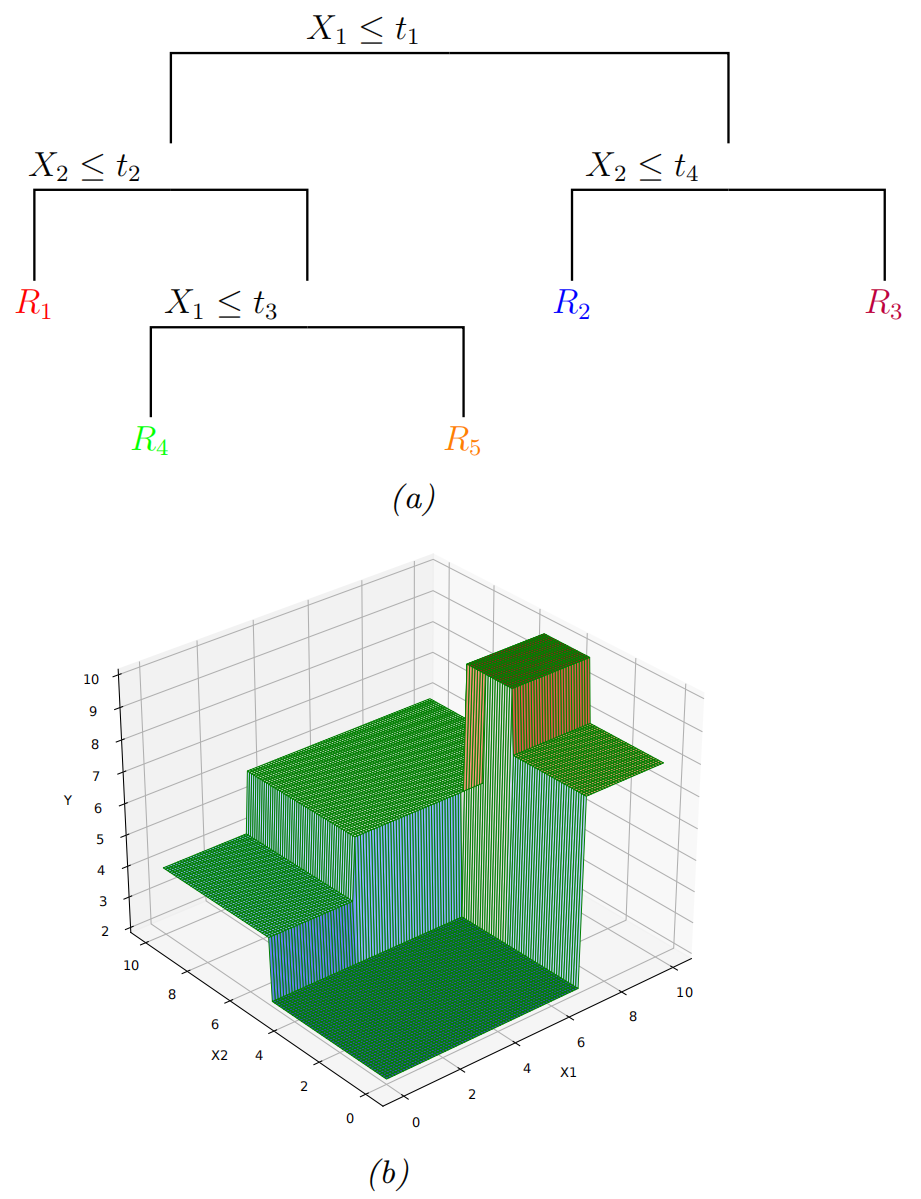
|
回归树:正式表述与训练
|
训练目标: 找到最大化均方误差 (MSE) 减少的切分。 分类变量输入: 切分比较特征 |
示例回顾
- 特征切分 — 大小 → 重量 → 颜色 — 将特征空间划分为区域
- 每个叶子的预测值
CART:分类树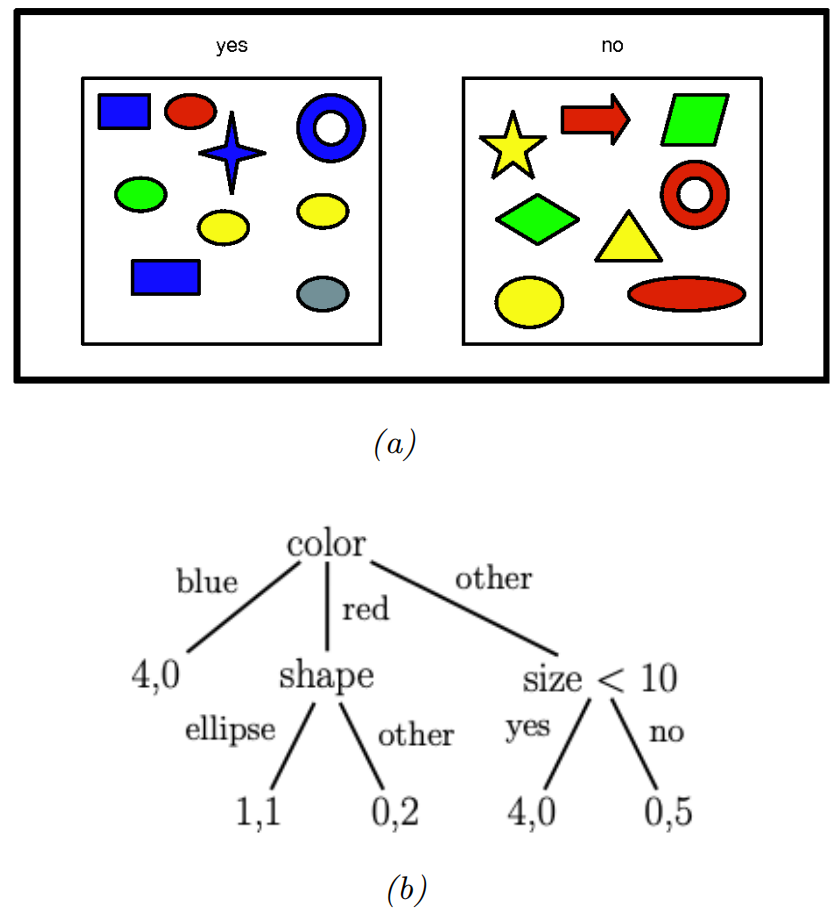
|
|
分类树:正式表述与训练
|
训练目标: 分类树在每个切分时最小化上切分的不纯度。常见的不纯度度量:
分类变量输入: 切分比较 |
示例回顾:
- 特征切分 — 颜色 → 形状 → 尺寸 — 将数据划分为区域
- 每个区域存储类别计数(例如,4 个是,0 个否),预测基于多数投票。
正则化
|
|
优缺点
|
|
集成学习:概述
-
核心思想:结合多个基础学习器以产生更强大、更稳定的模型。
- 单个模型并不完美 —— 它们可能具有高方差或偏差。
- 通过聚合多样化模型,随机错误往往会相互抵消。
-
为什么有效
- 误差分解: 相似的偏差 + 较低的方差(基础模型的独立性)
- 效果: 提高预测的稳定性、鲁棒性和泛化能力。
-
常见集成方法
类别 模型组合方式 目标 示例 平均法 独立地训练模型并平均或投票它们的预测 减少方差 Bagging, 随机森林 提升法 依次训练模型,每个模型聚焦于之前的错误 减少偏差 AdaBoost, 梯度提升 堆叠法 学习一个元模型以最佳地组合基础模型的输出 利用多样化学习者 堆叠, 混合
回归集成与分类集成
|
回归集成:平均预测
|
分类集成:投票或概率平均
|
基于平均的集成:Bagging
- 核心思想
- Bagging(自助聚合)是一种集成方法,它在不同的自助样本上训练多个基础模型,然后平均(或投票)它们的预测。
- 目的:降低具有高方差学习者(如树)的方差而不增加偏差。
- 算法(回归)
- 生成
- 每个样本从原始训练集的大小为
- 每个样本从原始训练集的大小为
- 在每个
- 进行预测:
- 生成
- 每个自助样本包含大约63% 独特的实例;剩下的**37%**是袋外 (OOB) 实例,对性能估计有用。
-
Bagging 有效的原因
- 对独立(或弱相关)模型进行平均抵消了随机波动的预测。
- 集成变得不那么敏感于任何单个训练样本 → 方差减少。
- 偏差大致保持不变。
-
注意
- OOB 预测可以在没有交叉验证的情况下估计测试集性能。
- Bagging 对于稳定学习者(例如线性模型)可能没有帮助,但对不稳定学习者(例如决策树)带来了很大好处。
- 下一个:随机森林通过引入特征级随机性来扩展 bagging。
随机森林:带有特征随机性的 Bagging
- 核心思想
- 随机森林通过在特征选择中增加随机性来扩展Bagging。
- 每棵树在数据的自助样本上进行训练,
在每个切分时仅考虑一个输入特征的随机子集。 - 目标:进一步降低树之间的相关性 → 更强的方差减少。
- 算法
- 对于每棵树
- 抽样自助数据集
- 构建决策树
- 在每个切分时,随机选择
- 仅在这
- 在每个切分时,随机选择
- 抽样自助数据集
- 预测通过平均(回归)或多数投票(分类):
- 对于每棵树
- 随机森林的帮助
- 去相关效果: 限制特征选择使树更加多样化,减少了标准 bagging 之外的集成方差。
- 偏差-方差权衡: 稍微增加偏差,但更大的方差减少 → 更好的测试性能。
- 可解释性奖励: 允许通过切分统计量或 OOB 错误影响来估计特征重要性。
- 注意
- 随机森林对噪声和过拟合非常稳健,即使有很多树。
- 当输入特征相关时,经验上优于普通的 bagging。
- 常见超参数:
- 树的数量
- 每次切分的特征数量
- 树深度和最小叶子大小
- 树的数量
提升:专注于偏差减少
- 核心思想
- 提升顺序构建集成,
每个新模型专注于之前的错误。 - 与 Bagging 或随机森林(并行且以方差为导向)不同,
提升是自适应的——后续模型经过训练以纠正先前的错误。
- 提升顺序构建集成,
- 机制
- 从一个简单的基础学习器
- 评估其在训练数据上的预测错误。
- 拟合下一个学习器
- 重复此过程进行
- 将所有学习器组合成加权和(或投票):
- 从一个简单的基础学习器
-
为什么提升有效
- 每个新学习器减少当前集成的剩余偏差。
- 重点顺序拟合允许模型捕捉之前遗漏的复杂模式。
- 只要每个基础学习器的表现略好于随机(弱学习器),
最终集成可以成为强学习器。
-
关键特性
方面 提升 Bagging / 随机森林 训练风格 顺序,自适应 并行 主要目标 减少偏差 减少方差 模型依赖性 后续模型依赖于先前的错误 模型独立训练 典型基础学习者 弱(例如,浅树) 不稳定(例如,深树) 示例算法 AdaBoost,梯度提升 Bagging,随机森林 -
注意
- 提升有时可能会在训练过长时过拟合——正则化和提前停止可以帮助解决。
- 最适合使用简单基础学习者,这些学习者单独拟合不足,但组合效果良好。
提升:序列学习算法
- 核心算法思想
- 提升训练一系列基础学习器
- 该过程为每个训练样本维护一个权重,随着训练进展,强调分类错误(或高误差)样本。
- 提升训练一系列基础学习器
- 通用提升过程(回归)
- 初始化: 对所有训练样本分配均等的权重
- 对
a. 在加权数据集上训练基础学习器
b. 计算加权错误
c. 确定学习器权重
d. 更新样本权重:增加错误分类样本的权重,减少正确样本的权重。
e. 规范化 - 组合学习器:
- 初始化: 对所有训练样本分配均等的权重
- 直觉
- 正确的预测在下一个步骤中降低了强调;困难的示例则获得更多关注。
- 每次迭代都调整模型容量,朝着之前错误的方向发展。
- 除了相比单一模型的系统性错误外,集成更具稳定性。
- 为什么有效
- 聚合多种弱学习者(略优于随机)为强组合模型。
- 权重机制像是一个残差校正过程,逐步减少偏差。
- 特别适合与灵活但简单的学习者(例如,浅树)。
- 注意
- 这个通用框架支撑了 AdaBoost(用于分类)和 梯度提升(用于回归或可微损失)。
前向阶段加性建模 (FSAM)
|
模型定义: 我们寻求一个加性模型,结合多个基础学习器:
|
优化框架: 我们以阶段性的方式最小化经验损失函数 在每个阶段
|
这是一个前向阶段加性的方法——每一步执行一个局部优化以减少总损失。
-
特殊情况
算法 损失函数 解释 AdaBoost 指数损失:%%BR%% 权重更新 梯度提升 任意可微损失 学习者拟合关于 -
总结
- FSAM 提供了提升算法的统一数学观点。
- 不同的提升方法仅在于它们的损失函数选择以及如何确定下一个学习者和步长。
- 该框架将“统计学习”和“优化”结合起来:提升
梯度提升:算法实施
|
核心思想
|
|
示例:二次损失与最小二乘提升
|
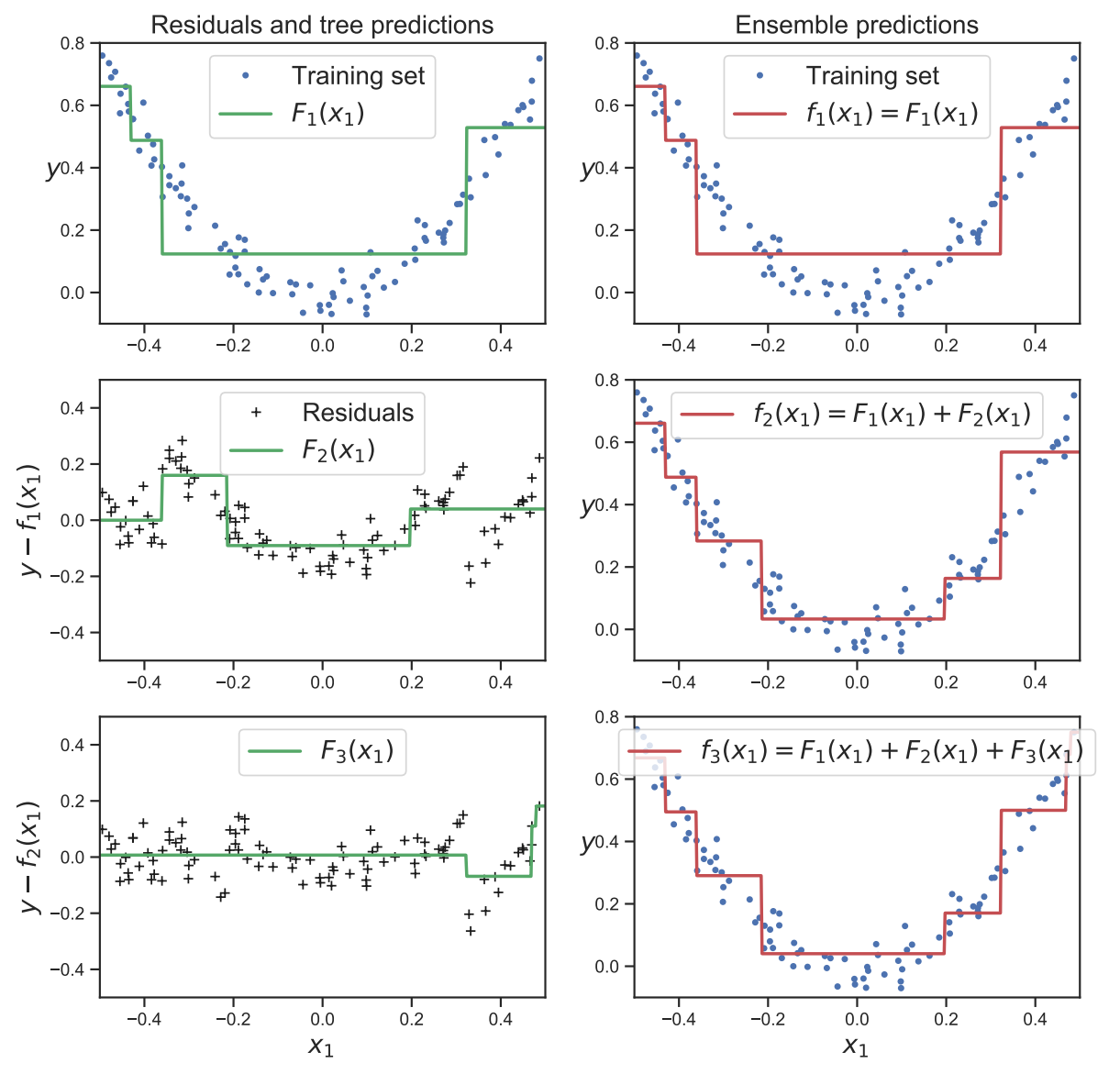
|
-
洞见
- 每个弱学习者纠正来自先前模型的错误方向。
- 步长
- 使用小的学习率,许多迭代→平滑优化轨迹。
- 提供一个灵活、损失无关的提升框架。
-
典型超参数
参数 作用 常见范围 提升轮数 100–1000 收缩步长 0.01–0.1 树的深度 基础学习者容量 3–8 子采样率 通过随机性进行正则化 0.5–1.0 -
注意
- 梯度提升包括如 GBDT, XGBoost, LightGBM 和 CatBoost 等流行算法。
- 适合于表格数据,但对超参数调整敏感。
梯度提升中的正则化与增强
-
为什么正则化很重要
- 经济和金融数据通常是噪声、非平稳且结构不稳定。
- 经典的梯度提升可能很容易过拟合训练数据,在新时期或市场环境中失去预测能力。
- 正则化旨在:控制模型复杂性;提高泛化能力;增强鲁棒性。
-
三种核心正则化技术
技术 关键思想 实践效果 金融研究实例 (1) 收缩(学习率) 减少每次迭代后的更新步长: 每个模型单独贡献较少。多次迭代→平滑收敛。 在信用风险建模中,较小的学习率(例如,0.05)防止模型过于激进地拟合极端或稀有的违约案例。 (2) 子采样(随机采样) 在每次迭代时使用训练数据的随机子集(例如,50–80%)。 引入随机性,降低方差。类似于随机梯度下降。 在高频交易预测中,随机子样本减少市场微观噪声,避免对瞬时模式的过拟合。 (3) 决策树约束(结构控制) 限制树的复杂性——深度、叶子数量或最小叶子大小。 减少模型的灵活性,控制过拟合。 在宏观经济预测中,使用浅树(深度 ≤ 4)防止模型对短期、非结构性波动做出反应。
-
实践中的正则化
- 这三种方法通常是一起使用。
- 常见配置:
- 学习率
- 子采样率 0.5–0.8
- 树深度 3–6
- 学习率
- 组合
-
实践启示:稳健性优于完美
研究背景 过拟合风险 推荐策略 信用评分(小样本、众多预测变量) 高 小学习率 + 浅树 宏观经济预测 中等 子采样 + 深度约束 市场操控 / 欺诈检测 非常高 强正则化 + 时间分段训练 投资组合风险建模 中等 保守参数 + 重复交叉验证
- 总结
- 正则化是实现稳健金融机器学习的关键。
- 收缩控制步长
- 子采样引入随机性
- 树约束限制模型复杂性。
- 结合使用可在结构变化与时变环境中稳定模型性能,确保结果保持经济可解释性和政策相关性。
- 正则化是实现稳健金融机器学习的关键。
堆叠:专注于模型多样性与跨模型协同
- 核心思想
- 堆叠通过一个更高层次的元模型,分层地组合来自多个不同算法的预测。
- 与 Bagging 或 Boosting(聚合类似的基础模型)不同,堆叠集成异质学习者——每个学习者捕获不同的结构或假设。
- 元模型学习如何信任每个基础学习者,依据其表现。
- 机制
- 将数据集分成几折(例如,通过 K 折交叉验证)。
- 训练不同的基础学习者(第 1 级模型):线性回归、随机森林、梯度提升、支持向量机、神经网络。
- 生成这些基模型的样本外预测。
- 将这些预测用作元特征来训练元模型(第 2 级),通常为线性回归或正则化学习者。
- 最终预测:
-
为什么堆叠有效
- 不同的算法学习了金融数据的互补方面 — 例如,线性结构、阈值效应或交互项。
- 元模型平衡它们的优势,纠正任何单一模型的系统性错误。
- 通过整合多种视角,堆叠可以实现:
- 更高的鲁棒性,对模型错误指定的抵抗力
- 更好的样本外泛化能力
- 降低对单个模型偏差的依赖
-
关键特性
方面 堆叠 Bagging Boosting 架构 分层(多级) 并行 顺序 基础模型 异质(不同类型) 同质 同质 依赖性 元模型依赖于基础输出 独立 步骤依赖 主要目标 结合多样化建模优势 减少方差 减少偏差 示例元模型 线性 / 岭回归 – –
- 注意事项
- 堆叠需要小心的数据划分以避免信息泄露。
- 计算负担较重,但概念灵活——适用于回归、分类或时间序列任务。
- 在金融领域尤其有用,结合线性(基于经济理论)和非线性(基于数据驱动)模型往往能提高稳定性。
堆叠实施细节
|
数据划分策略 — 避免信息泄露
|
基础模型 — 如何选择
设计原则: 选择多样化但互补的学习者,以反映不同的经济结构。 |
-
元模型 — 如何训练
- 目标: 学习基础预测的最佳组合。
- 常见选项:
- 线性 / 岭回归 — 可解释、低方差。
- 弹性网 / LASSO — 强制基础模型之间的稀疏性。
- 简单树或GBM — 当关系非线性时灵活。
- 元模型应比基础模型简单,专注于聚合而非重新发现模式。
-
工作流程概述
第1步 将数据划分为训练折 第2步 训练多样化的基础模型 → 获取样本外预测 第3步 从基础预测中构建元特征 第4步 在这些元特征上训练元模型 第5步 将训练好的管道应用于测试数据或新的时间段
- 示例:投资组合风险预测
- 目标: 预测1个月后的投资组合波动性。
- 基础模型:
- 线性 GARCH(1,1): 捕捉条件方差
- 随机森林: 利用非线性收益–因子关系
- XGBoost: 强调尾部风险和稀有事件
- 元模型:
- 岭回归,在五折样本外预测上进行训练
- 结果:相比任何单一模型,提高了稳定性并减少了假波动尖峰。
-
常见陷阱
问题 描述 缓解措施 数据泄露 元模型使用了样本内预测 严格的折叠分离或滚动窗口设置 过于复杂的元模型 学习基础模型噪声而非信号 使用正则化回归 样本量有限 观察数量太少以估计第二层 减少基础模型数量或折叠数 不一致的缩放 基础模型输出在不同的尺度上 在元训练前进行标准化 -
总结
- 合理的数据划分至关重要 — 没有它,堆叠将失败。
- 基础模型提供结构多样性;元模型提供自适应综合。
- 在金融领域,这种分层设计支持强大的跨制度预测和更好的经济可解释性。
集成学习概述 — Bagging、Boosting、Stacking
-
三种主要方法一览
方面 Bagging Boosting Stacking 核心策略 并行重采样和投票 顺序错误校正 分层模型集成 模型依赖性 独立学习者 每个学习者依赖于先前的错误 元级依赖于基础输出 主要目标 减少方差 减少偏差 结合多样化模型优势 典型基础学习者 不稳定模型(例如,深树) 弱模型(例如,浅树) 混合模型(线性 + 非线性) 组合规则 平均 / 投票 加权加法更新 元模型学习最佳权重 代表性算法 随机森林 AdaBoost、GBM、XGBoost 堆叠泛化 偏差–方差–多样性视角 ↓ 方差 ↓ 偏差 ↑ 模型多样性
-
它们如何相辅相成
- Bagging / 随机森林: 通过重采样稳定高方差估计器。 → 可靠的高维数据,例如情感分数、市场特征。
- Boosting: 迭代地优化弱学习者,关注困难样本。 → 在信用评分或评级预测等信号微弱或非线性情况下有效。
- Stacking: 集成不同性质的模型(计量经济模型与机器学习模型) → 适用于复杂多结构问题,如 GDP 预测或系统风险指数。
-
金融与经济应用的指导
场景 首选方法 理由/目标 信用风险建模 %%BR%%(不平衡标签、表格数据) Boosting(例如,XGBoost) 专注于难以分类的违约;处理特征交互。 宏观经济预测 %%BR%%(少量特征、时间结构) Bagging / 随机森林 降低小样本的方差;对异常值鲁棒。 市场微观数据或多源模型 %%BR%%(价格、文本、基本面) Stacking 集成异质模型;结合可解释性和灵活性。 投资组合优化或波动率预测 Stacking / Bagging 混合 在多个制度之间平衡预测稳定性与适应性。
- 主要结论
- 所有集成方法都共享相同的哲学:多个弱模型 → 集体力量。
- 它们的区别在于如何构建集成多样性:
- Bagging: 通过数据重采样(方差减少)
- Boosting: 通过迭代聚焦(偏差减少)
- Stacking: 通过模型异质性(多样性融合)
- 在金融研究中,它们共同支持稳健的、适应制度转变的预测,并鼓励模型多元化 — 这在实证经济学中是一个重要原则。
第 4 部分 · 无监督学习
动机
- 探索金融数据中的潜在结构与隐藏因子。
- 降维简化复杂系统,聚类揭示市场模式与投资者群体。
- 支撑风险分层与因子提取的前期分析。
无监督学习作为数据驱动的结构发现探索,旨在金融系统中发现潜在结构。
无监督学习 — 介绍与核心思想
-
从有监督到无监督
- 有监督学习: 从标记数据中学习映射
- 无监督学习: 探索数据自身的结构(旨在实现发现、压缩和表示)。
- 没有预定义的结果变量;模型揭示隐藏的模式、群体或关系。
- 有监督学习: 从标记数据中学习映射
-
核心哲学
有监督 无监督 从已知目标 仅从输入结构学习 目标:最小化错误或损失 目标:最大化模式清晰度或紧凑性 典型任务:回归,分类 典型任务:聚类,降维,异常检测,关联规则 侧重于预测 侧重于理解 / 探索
-
示例直觉
- 聚类: 将具有相似模式的公司或客户分组。 → “哪些实体表现相似?”
- 降维: 提取驱动变化的关键因子。 → “什么潜在力量使这些变量共同变化?”
- 关联规则: 查找共同发生的事件。 → “如果 X 发生,Y 可能会跟随吗?”
- 异常检测: 识别罕见或异常行为。 → “哪个时间段或公司看起来不寻常?”
-
在金融与经济中的重要性
应用领域 示例用例 益处 市场结构分析 识别具有相似收益行为的股票组 揭示行业共动性 消费者金融/信用 按消费和还款模式将借款人分组 更好的细分,风险分析 宏观经济学 从多个指标中提取隐藏的经济因子 简化大数据集供政策分析 欺诈/危机检测 发现交易或宏观趋势中的异常 早期预警和控制
-
概念类比
有监督 → 教师提供正确答案 无监督 → 学生自我组织成学习小组“教师”(标签)缺席——然而洞察力从数据点之间的关系中出现。
这使得无监督方法非常适合探索性分析和假设生成。 -
过渡
在接下来的页面中,我们将探索主要的无监督方法:
- 聚类 → 发现相似性结构,
- 降维 → 总结复杂变量,
- 关联规则与异常检测 → 发现隐藏关系与异常值。
这些技术将原始、未标记的数据转变为可解释的经济知识。
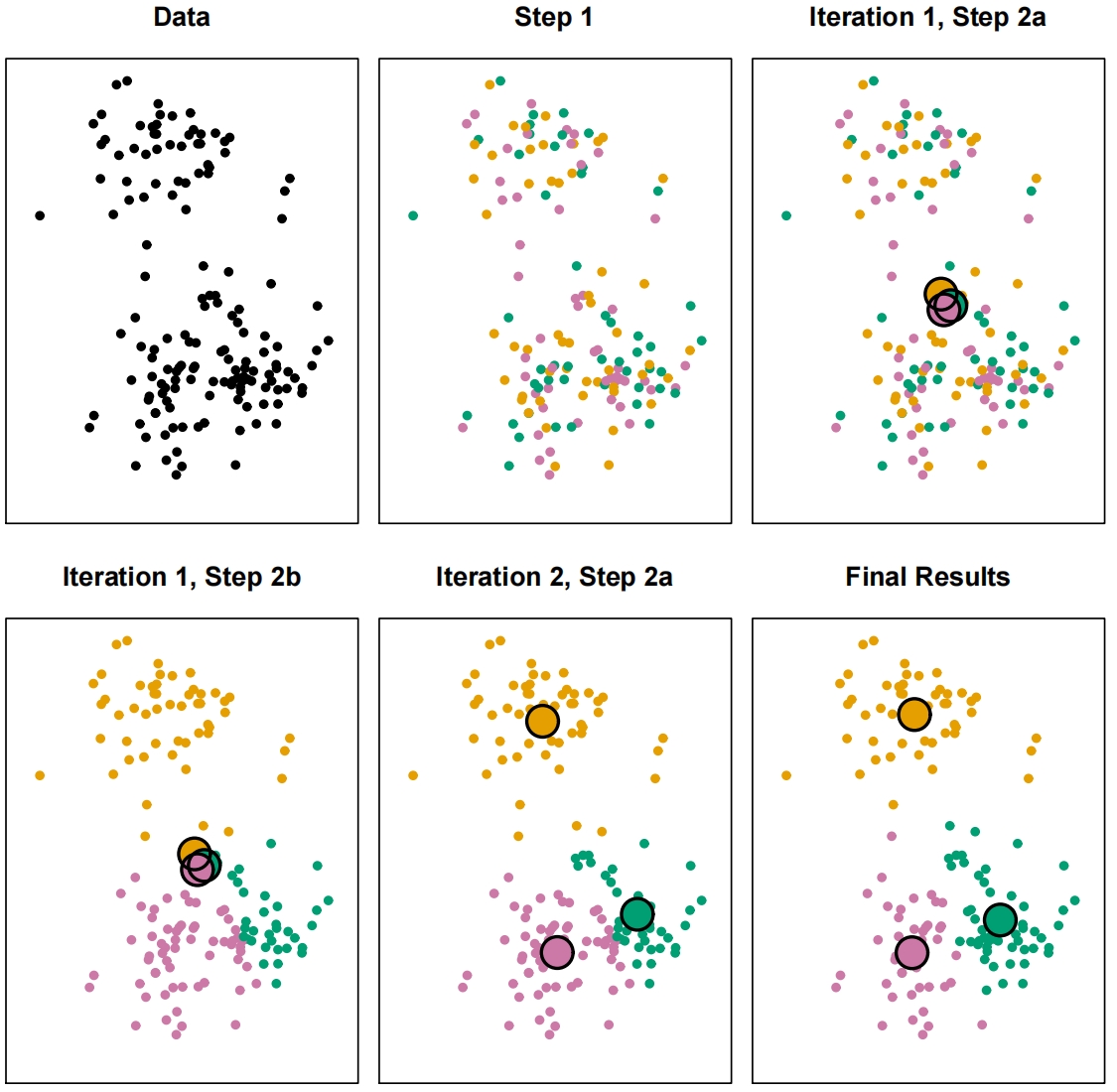
聚类方法概述 (K‑Means、层次聚类、DBSCAN)
- 聚类的核心思想
- 目标: 将观察值分为聚类,使同一聚类中的对象是相似的,而不同聚类中的对象是不相似的。
- “相似性”的定义取决于距离度量(例如,欧几里得、余弦、马氏距离)。
- 聚类提供数据的结构视图,帮助识别潜在群体或状态。
-
主要方法
方法 关键原则 优势 局限性 K‑Means 最小化聚类内方差(惯性) 快速、简单、广泛使用 必须预先指定K;对规模和异常值敏感 层次聚类 根据距离链接(单、全、平均)合并或拆分聚类 可视化树状图;不需预设K 对于大N 计算负担沉重 DBSCAN 基于密度:聚类是稠密区域,由稀疏区域分开的 检测不规则形状和噪声 需要参数调优(ε,MinPts)
K-Means 聚类
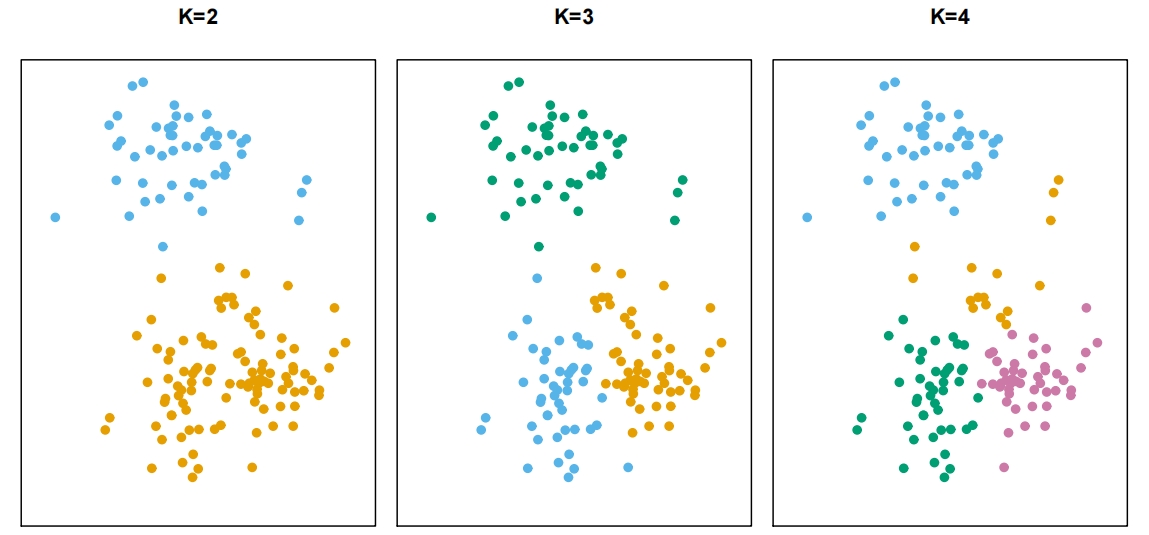
- 将数据集划分为
- 令
-
-
-
- 大思想
- 聚类内变异尽可能小
- 聚类内变异
|
|
-
如何选择方法
数据特征 推荐方法 理由 明确的聚类边界,近似球形 K‑Means 高效,稳定中心 未知组数,需层次结构 层次聚类 揭示嵌套结构 存在不规则形状或噪声 DBSCAN 基于密度的鲁棒性 非常大的 N,高维 先使用 MiniBatch K‑Means 可扩展的近似
评估聚类质量
- 惯性 / 聚类内 SSE → 凝聚度指标
- 轮廓系数(−1→1) → 指点是否适合分配的聚类
- 肘部法 → 选择 K 的可视化方式
- 通过领域洞察验证 → 检查聚类是否具有经济意义
在金融应用中,聚类的可解释性与数值紧凑性同样重要。
-
金融与经济相关性
领域 示例用途 结果 金融市场 按收益相关性对股票或投资者分组 识别市场状态或风格聚类 消费者行为 按交易历史对客户进行细分 目标营销和信用策略 宏观政策 按宏观指标对国家进行聚类 揭示结构相似性或差异
经济学中的聚类 — 市场细分示例
- 目标
- 演示如何聚类帮助识别经济或市场数据中的隐藏结构。
- 示例:市场细分 — 按行为或财务相似性对公司(或消费者)进行分组。
- 目标:获得不同的数据驱动“细分”,而非任意类别。
聚类结构通常揭示潜在制度或商业策略,这些在简单平均值中是不可见的。
-
示例数据集
实体 用于聚类的特征 经济含义 公司 (市场营销 / 零售) 销售增长、广告比例、产品多样性、数字渠道使用 反映市场行为和创新强度 消费者 (金融 / 银行) 消费频率、平均交易额、信用利用率 揭示不同的消费/风险特征 股票 (市场数据) 平均收益、波动率、换手率、与指数相关性 识别风格聚类或行为状态 标准化至关重要 — 在聚类之前将所有特征缩放至可比较单位。
- 应用 K‑Means
-
工作流程
- 预处理数据(去除异常值,标准化特征)。
- 通过 肘部法 或 轮廓得分 选择
- 将 K‑Means 拟合到数据集 ⇒ 获得聚类分配。
- 描述每个聚类 → 解释经济含义。
-
说明性结果
聚类 ID 概要描述 代表行为 1 高销售额 & 高数字化使用 数字领袖 2 中等增长 & 传统渠道 常规参与者 3 小型公司,低市场支出 细分生存者
-
-
经济解释
- 市场细分 提供了超越描述性平均值的可操作洞察:
- 策略目标(对每个细分采取不同的定价或产品线)。
- 投资分类(增长 vs. 价值 vs. 数字动量)。
- 政策评估(某些市场群体是否滞后或领先?)。
- 聚类形成了一种数据驱动的分类法, enabling 更细致的分析。
在研究层面,聚类可以作为后续模型的无监督标记机制。
- 市场细分 提供了超越描述性平均值的可操作洞察:
-
扩展思路
方向 在经济研究中的目的 随时间变化的聚类稳定性 研究结构变化或市场状态转变 聚类转移矩阵 评估典型行为类型之间的流动性 与有监督模型结合 使用聚类标签作为解释变量或控制变量 混合方法(K‑Means + DBSCAN) 同时捕捉核心群体和边缘异常
降维 — PCA 和 t‑SNE
|
|
-
降维 在保留数据最重要的方差或结构的同时压缩数据。
-
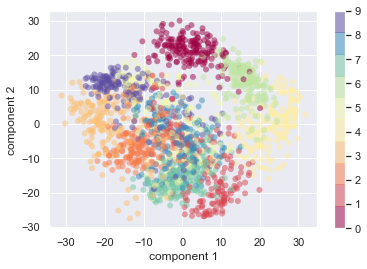
两种主要哲学: 主成分分析(PCA)和t-分布随机邻居嵌入(t‑SNE)
方法 类型 关键思想 输出空间 PCA 线性投影 旋转轴以最大化解释的方差 成分是原始变量的线性组合 t‑SNE 非线性流形学习 在低维空间中保留局部邻居关系 适合可视化的2维/3维嵌入
- 示例:手写数字识别(28*28维到2维)
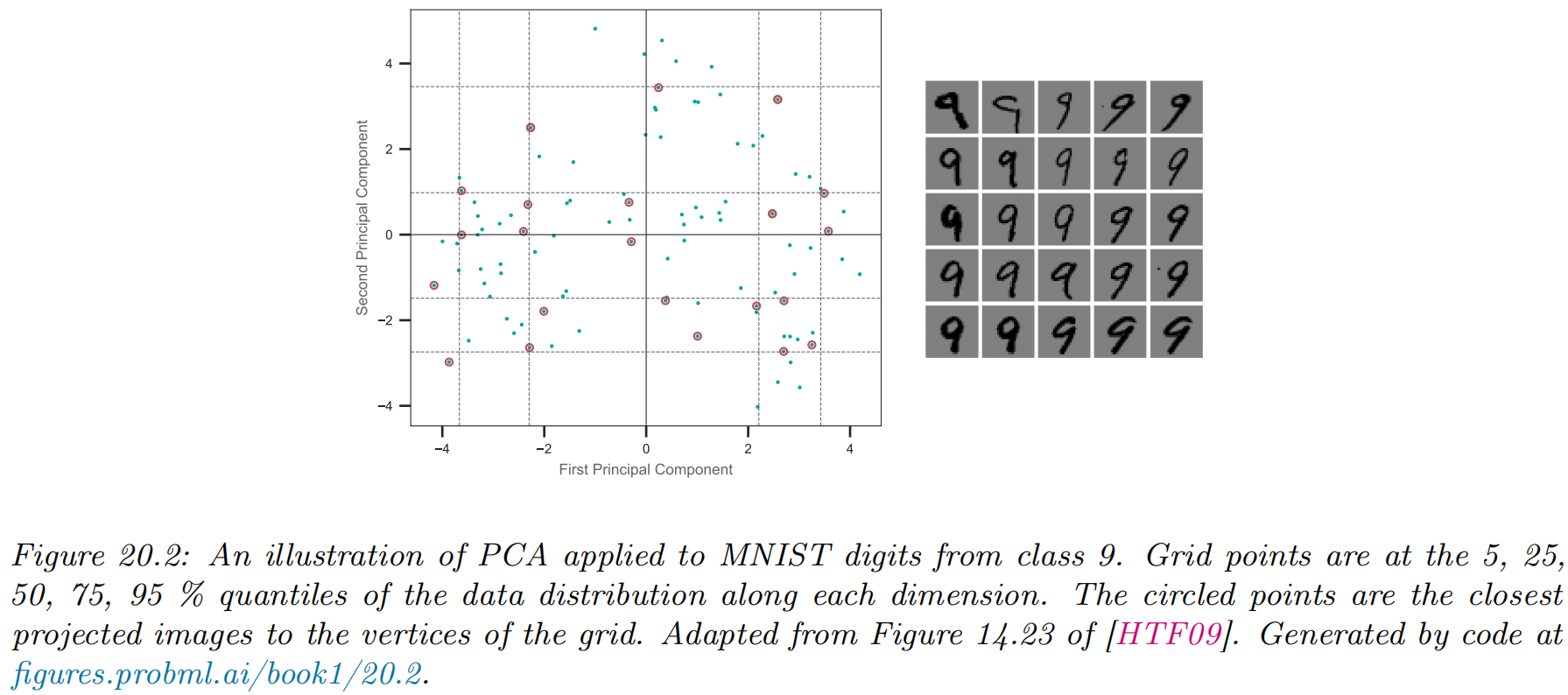
- 示例:人脸识别(64*64维到3维)

-
PCA — 核心机制
- 标准化变量
- 计算 协方差矩阵
- 求解 特征值问题
- 根据特征值对特征向量排序 → 主要成分。
- 标准化变量
-
示例解释:
- PC1 → “整体经济活动因子”
- PC2 → “通货膨胀与增长权衡”
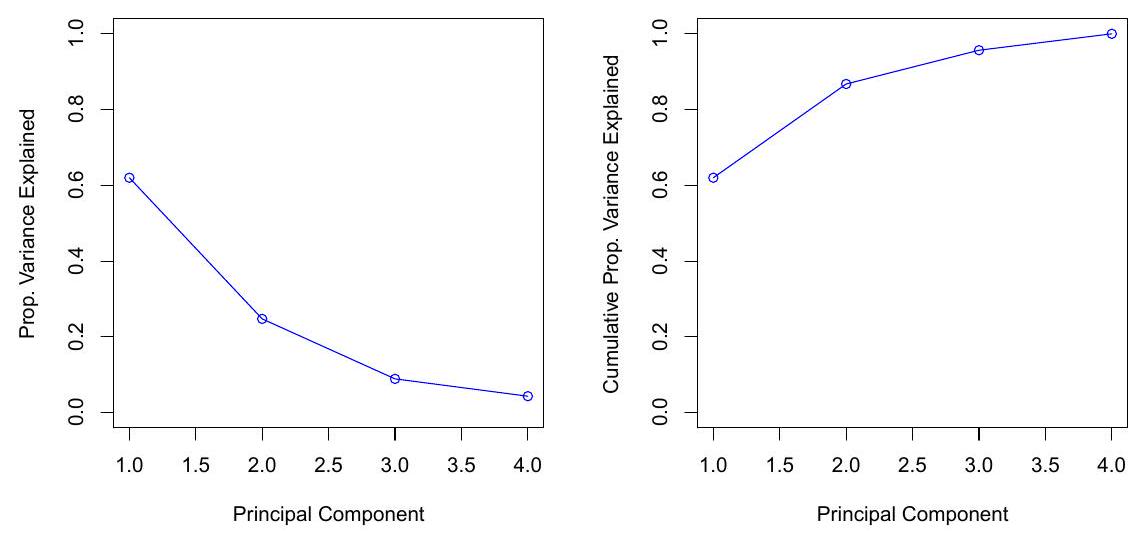
- 前几个PC解释的方差 = 数据压缩效率。
PCA揭示了潜在正交方向,这些方向最佳地总结了数据集。
|
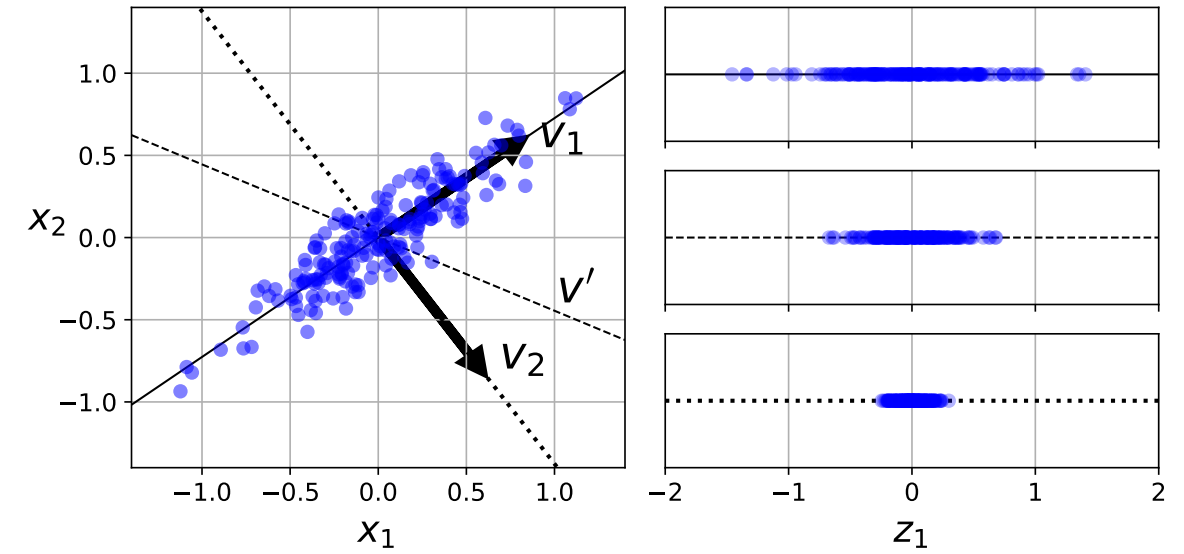
|
- 主成分的另一个解释: 主成分提供了与观察结果最接近的低维线性表面。
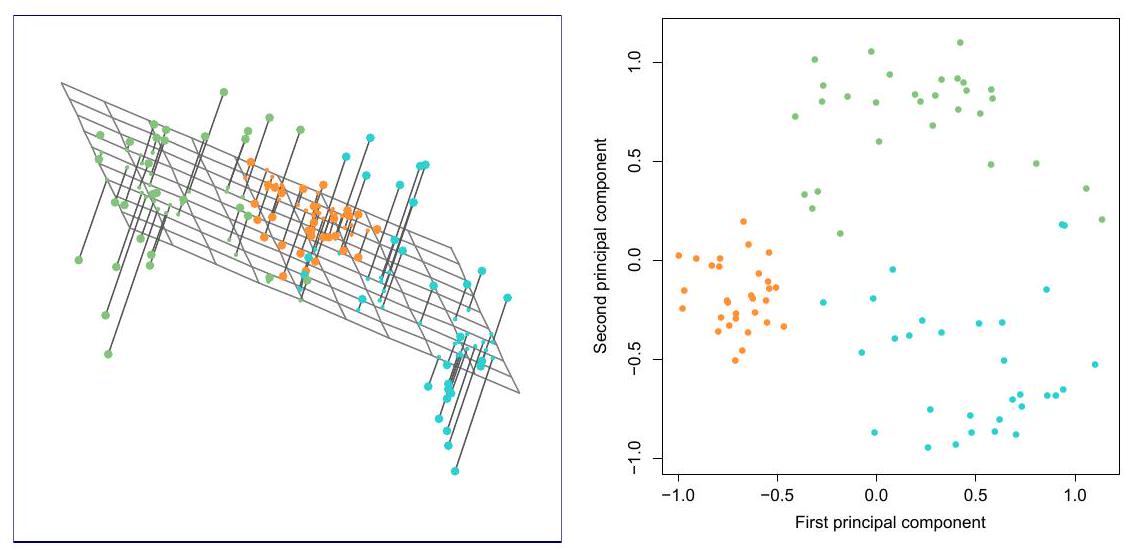
- 对于第
- 优化问题
- 目标的最小可能值为
- 当
- 解释的方差比例(PVE)
- 数据集中存在的总方差定义为
- 第
- 第
- 数据集中存在的总方差定义为
-
数据的方差可以分解为前
数 据 的 方 差 前 个 主 成 分 的 方 差 的 维 近 似 -
我们可以将 PVE 解释为由前
- 代码:可视化
|
|
t‑SNE — 直观图示
|
|
-
比较概述
方面 PCA t‑SNE 线性/非线性 线性 非线性 目标 最大化全局方差 保留局部相似性 输出可解释性 高 低(无明确因子) 用例 因子提取,噪声减少 可视化探索,聚类辅助 运行时可扩展性 非常快 对大型 N 较慢
-
金融与经济应用
上下文 如何使用 洞察结果 宏观经济学 将100多个指标减少为几个主成分 识别潜在经济周期或冲击 投资组合风险 通过 PCA 分解协方差矩阵 揭示主导风险因子(市场、规模、行业) ESG 分析 压缩数十个评分为一个复合评分 构建可解释的可持续性指数 消费者分析/文本数据 可视化消费或意见的相似性 发现行为聚类
PCA 在金融中的应用 — 因子分析与风险分解
|
动机
|
从回报到因子
|
-
主成分的经济解释
主成分 可能的经济含义 典型模式 PC1 市场广泛因子 解释最大的价格波动部分,与指数高度相关。 PC2 行业轮换因子 区分周期性与防御性产业。 PC3 规模或流动性因子 捕捉小与大或流动与非流动对比。
投资组合风险分解
每个项对应一个主成分对投资组合风险的贡献。
| 成分 | 方差份额 | 解释 |
|---|---|---|
| PC1 | 52% | 系统性市场风险 |
| PC2 | 18% | 行业轮换风险 |
| PC3+ | 30% | 特殊或噪声 |
关联规则学习 — 零售市场篮子分析
|
核心思想 关联规则学习发现商品或事件之间的共现模式:
最初用于零售(购物篮),它在经济和金融中有广泛应用——从消费者分析到交易网络和风险事件检测。 |
示例场景 在一家超市的交易数据集中:
目标 → 寻找规则,例如:{面包, 牛奶} → {啤酒},这意味着购买面包和牛奶的顾客通常也购买啤酒。 |
- 规则指标
| 度量 | 公式 | 含义 |
|---|---|---|
| 支持度 | 包含A和B的交易频率 | |
| 置信度 | 给定A的条件下B的概率 | |
| 提升率 | 超越机会的关联强度(>1 = 正相关) |
示例:如果提升率 = 1.8,购买A的顾客有80%的概率同时购买B,超过平均水平。
-
Apriori 算法
- 生成超出最小支持度的频繁项集。
- 递增扩展组合(广度优先)。
- 产生高置信度关联规则。
使用“Apriori 属性”:频繁项集的所有子集也必须是频繁的。
热门扩展: FP‑Growth、ECLAT用于可扩展性。
-
超越零售的应用
领域 数据来源 获得的洞察 电子商务/银行 购买或交易日志 交叉销售与推荐 宏观经济学 国家宏观指标
(例如,通货膨胀↑ & 能源价格↑ → 政策收紧)检测共同运动的模式 金融与风险 欺诈或损失事件日志 共发生触发因素分析 文本分析 关键词或主题共现 识别潜在问题关联
经济背景下的解释
- 在行为经济学中:帮助理解消费模式。
- 在金融中:支持产品捆绑或事件相关性分析
(例如,政策冲击与某些市场反应的共发生)。 - 在政策制定中:识别在某些结果前的频繁指标组合(例如,通货膨胀↑ + 进口↓ → 衰退信号)。
异常检测 — 欺诈与危机的预警
- 异常(离群值) = 与数据的预期模式强烈偏离的观察。
- 在金融和经济中,异常通常表明不规则行为、欺诈或结构性危机。
- 异常检测的任务:
- 定义什么是正常(基于数据分布或相似度)。
- 测量与该正常区域的偏差。
- 标记可疑或稀有事件以供进一步分析。
-
典型的经济与金融背景
领域 异常示例 检测的价值 银行与支付 不寻常的交易模式或金额 防范欺诈,反洗钱系统 金融市场 异常回报或波动性飙升 市场压力的早期信号 宏观经济学 指标的突然偏离(例如,信用与增长) 危机的早期预警 公司金融 意外的会计数字 治理与审计检查 当标记的欺诈或危机数据有限时,无监督的异常检测至关重要。
-
主要方法
方法 机制 何时使用 统计阈值 识别远离均值的点(z‑得分,IQR 规则) 小数据集,可解释 基于距离的方法 计算最近邻→标记孤立点 中等数据集,清晰度量空间 基于密度的(DBSCAN / LOF) 低密度 = 异常 非线性结构 基于模型(一类SVM,孤立森林) 学习“正常”区域的边界 高维/复杂数据 孤立森林关键思想: 随机划分数据;异常需要更少的分割来隔离。
定量评估
| 指标 | 含义 |
|---|---|
| 精确率/召回率 | 错过和假检测之间的权衡 |
| ROC/PR 曲线 | 如果部分标签存在,评估模型区分能力 |
| 经济验证 | 检查标记的异常是否与已知事件一致(例如,金融危机2008,COVID冲击) |
-
经济解释
- 欺诈检测:
- 分析交易图;找到具有稀有模式的用户或账户。
- 使用异常得分作为风险指标仪表盘的一部分。
- 危机早警:
- 监控宏观指标在PCA简化空间下的异常值 → 潜在系统性风险时期。
- 结合波动性、利差指数或信用杠杆的阈值。
在这两种情况下,异常 = “重大事件前的弱信号”。
- 欺诈检测:
-
混合与实际系统
- 混合管道: 将无监督检测与基于规则的警报与专家反馈循环相结合。
- 时间维度: 随时间跟踪聚类或异常得分揭示动态,而不仅仅是静态模式。
- 可视化: 热图或动态得分图表帮助决策者解释突发偏差。
总结 — 无监督学习在经济研究中的应用
-
我们学到了什么
- 无监督学习 ≠ 预测 — 它关于发现。
- 在本讲中,我们探讨了数据——在没有明确标签的情况下——如何揭示结构、模式和信号。
方法家族 主要目标 经济含义 聚类 组群相似的观察 市场细分/结构制度识别 降维(PCA / t‑SNE) 压缩信息,提取潜在成分 因子提取/风险分解 关联规则 发现共生逻辑 行为关联/政策指标关系 异常检测 识别不规律的样本 欺诈筛查/危机早期信号 共同主题:在显然的随机中找到秩序。
-
概念整合
- 模式发现
- 无监督方法揭示了数据的几何结构—其聚类、方向和密度。
- 这些成为后续监督模型或经济解释的基础。
- 数据表示: 像PCA和嵌入方法的技术将杂乱的、重叠的变量转化为可解释、紧凑的维度。
- 信号检测: 异常和关联方法生成早期信号,传统计量经济学可能错过。
- 模式发现
-
经济分析中的优势
方面 无监督学习的附加价值 探索性能力 在设定假设之前揭示潜在结构 可扩展性 处理大型、多维数据集 适应性 即使在有限或没有标记的数据上工作 互补性 增强传统的计量经济模型(例如,因子分析、结构突变) 特别在像金融和政策分析这样的“数据丰富、理论稀缺”的环境中非常有价值。
-
方法论反思
- 可解释性重要: 经济含义必须与统计输出相伴。
- 没有免费的午餐: 不同的算法适合于不同的数据形状;验证至关重要。
- 混合建模: 将无监督表现与监督预测结合可增强稳健性。
- 时间维度: 随时间跟踪聚类或异常得分揭示动态,而不只是静态模式。
-
实践实施检查表
- 数据预处理 — 标准化,去除异常值
- 选择适合目标的算法(分组、降维、关联、检测)
- 评估统计拟合与经济逻辑
- 可视化 → 解释 → 与领域知识验证
一直将算法视作透镜,而非绝对真理。
PCR - 核心思想
- 两步程序: “先通过方差压缩,再回归”
- 应用**主成分分析 (PCA)**于
- 在OLS中采用前
- 应用**主成分分析 (PCA)**于
- 关键: PCR在构建子空间时对
- 直觉:
- 如果
- 如果
- 如果
|
设
等价于对 |
视为投影:
偏差—方差机制:
|
PCR - 算法
| 步骤 | 描述 |
|---|---|
| 1️ | 标准化 |
| 2️ | 计算特征向量 P 的协方差矩阵 Σₓ = X'X / n |
| 3️ | 保留前 K 主成分 T = X Pₖ |
| 4️ | 对 T 回归 Y |
| 5️ | 获得拟合的 β = Pₖ βₜ |
选择
- 交叉验证
- 累积解释方差阈值
PCR 在金融中的应用
解释: PCR 强调方差结构,而不是预测相关性 → 用于描述性因子发现。 |
适用情况:
失效情况:
要点:
|
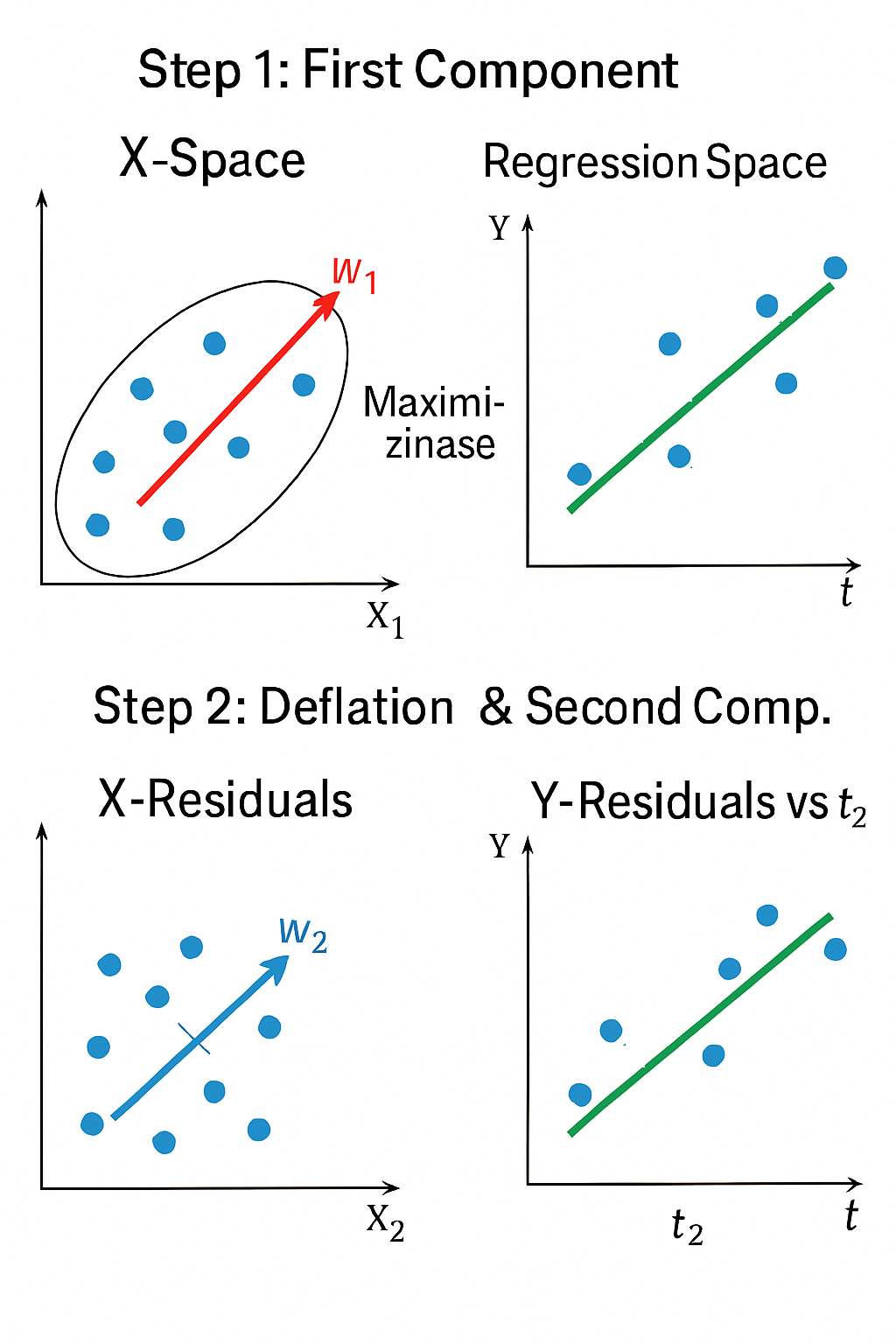
PLS - 核心思想
|
PLS使用 第一成分:
解释:
|
|
PLS — 核心思想(代数与算法)
逐成分(NIPALS/SIMPLS思路):
- 对
- 消减:
- 循环至
其中
Krylov子空间视图:
- PLS将
- 随着
PLS与PCR的比较
|
几何
与相关方法的链接:
|
收缩特征:
影响:
|
财务中的实际影响
-
资产定价因子:
- PCR → 解释结构因子(水平/斜率/曲率)
- PLS → 预测因子用于回报/风险溢价
-
宏观预测:
- PCR → 概括广泛变异的“超级数据”指数
- PLS → 针对特定目标(例如,通货膨胀、超额回报)进行预测的指数
-
信用风险:
- 在许多相关比率弱预测PD时,PLS往往表现出色
选择 K(PCR 和 PLS)
- 在预测损失上进行交叉验证(样本外 R²,MSPE)
- 针对组件的信息标准(回归中 BIC)
- 跨子样本/时间框架的稳定性检查
- 对于时间序列:将
预处理:
- 始终标准化
- 适当时考虑去除公司/时间固定效应
PCR与PLS的直觉与比较
| 特征 | PCR | PLS |
|---|---|---|
| 使用 |
否 | 是 |
| 目标 | ||
| 预测能力 | 中等 | 较高 |
| 可解释性 | 高 | 中等 |
| 典型目标 | 数据总结 | 预测 |
在金融计量经济学中,PLS经常产生更能预测回报或宏观变量的因子。
PCR vs PLS vs 正则化方法
| 方法 | 降维机制 | 使用 |
变量选择 | 可解释性 | 预测准确性 |
|---|---|---|---|---|---|
| PCR | PCA在 |
中等 | |||
| PLS | 中等 | 高 | |||
| LASSO | 稀疏 | 高 | |||
| Ridge | 稳定 | 中等 | |||
| Elastic Net | 中等 | 高 |
实证指南方法选择
| 研究目标 | 数据结构 | 推荐方法 | 理由 |
|---|---|---|---|
| 解释结构关系 | 中等维度 | PCR | 捕捉潜在数据结构 |
| 预测 |
高度共线性 | PLS | 使用 |
| 特征选择/大量 p | 稀疏相关信号 | LASSO/Elastic Net | 自动变量选择 |
| 稳定估计/共线性 | p≈n大 | Ridge/PLS | 收缩稳定估计 |
| 混合目标(解释+预测) | 高维、噪声 |
混合PLS+正则化 | 在金融中的新兴趋势 |
总结 — 核心思想
- PCR: 将β投影到X的顶级方差子空间;对于结构良好,若信号≠方差则风险较大
- PLS: 逐步提取最大化与y协方差的X方向;通常在小K时更具预测性
- 两者通过控制维度减少方差;PLS利用Y引导子空间
经验法则:
- 想要可解释的结构 → PCR
- 想要少量成分的早期预测能力 → PLS
- 如果p ≫ n且选择重要,比较LASSO/EN;混合PLS + 正则化是强基线
总结与阅读
-
总结 · 第 02 讲
主题 精髓 金融应用 回归 线性 + 正则化模型用于连续目标 回报 & 风险预测 分类 基于特征的二元决策 信贷评分,欺诈检测 基于树的模型 集成方法(GBM,RF)用于准确性与可解释性 PD建模,风险评级 无监督学习 聚类 & PCA 发现隐藏模式 制度分析,因子提取 浅层学习为后来的深度学习方法奠定了基础。
推荐阅读
- Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani, Jonathan Taylor. 《统计学习导论及其在Python中的应用》[M]。Springer Cham,2023。
- Murphy K P. 《概率机器学习:导论》[M]。MIT出版社,2022。
- Gaillac C, L'Hour J. 《机器学习与计量经济学》[M]。牛津大学出版社,2025。
最终收获
- 浅层学习算法构成了金融预测与决策的核心基础。
- 回归、分类、树模型与无监督学习共同支撑“结构化分析 + 可解释建模”。
- 下一讲:深度学习与金融中的表现学习
→ 利用CNN、RNN与自编码模型处理时序与非结构化金融数据。