随机过程的概率性质
- 条件分布
- 随机过程
- 确定随机过程分布特性的核心问题:“给定当前状态的未来概率分布是什么?”
- 随机过程
- 均值与协方差
- 均值函数:
- 自协方差函数:
- 均值函数:
- 平稳过程
- 定义:概率性质(均值、方差、协方差)与时间无关的过程。
- 应用:平稳过程是很多金融模型的出发点。
马尔可夫过程(Markov Processes)与金融市场
-
定义:一个随机过程
-
无记忆性:未来只依赖于当前状态,与历史状态无关
-
弱式有效市场与马尔可夫过程
- 基于市场历史数据制定交易规则不能持续获得超额收益,技术分析无效
- 讨论:
- 市场弱式有效,股票价格是否为马氏过程?
- 市场弱式有效,股票指数是否为马氏过程?
布朗运动(Brownian Motion)

|
|
布朗运动的性质
-
观察:花粉颗粒运动轨迹完全随机但有统计规律
-
物理本质
- 观察非连续
- 观察窗内微小颗粒在水中被无数水分子随机撞击
- 中心极限定理
-
数学特性
- 起点固定:
- 独立增量:不同时间区间的变化相互独立
- 正态分布增量:
- 路径连续:时间轴上没有跳跃
- 非平滑轨迹:路径在任何点都不可微
- 起点固定:
布朗运动与金融模型
-
讨论:花粉颗粒的布朗运动与金融资产价格变化的机制有相似性吗?
-
布朗运动的金融应用
- 资产价格建模:标准布朗运动是几何布朗运动(用于股票价格建模)的基础
- 随机波动性:捕捉金融市场的不确定性
- 期权定价:Black-Scholes模型的核心组成部分
- 风险管理:用于模拟市场风险情景
布朗运动/维纳过程的数学定义
-
一个随机过程
- 初始值为0:
- 高斯增量:记
- 增量独立:两段不同(无重叠)时间
- 路径连续:轨迹没有跳跃
- 初始值为0:
-
维纳过程的性质
- 均值:
- 方差:
- 马尔可夫性
- 均值:
广义维纳过程(Generalized Wiener Processes)
|
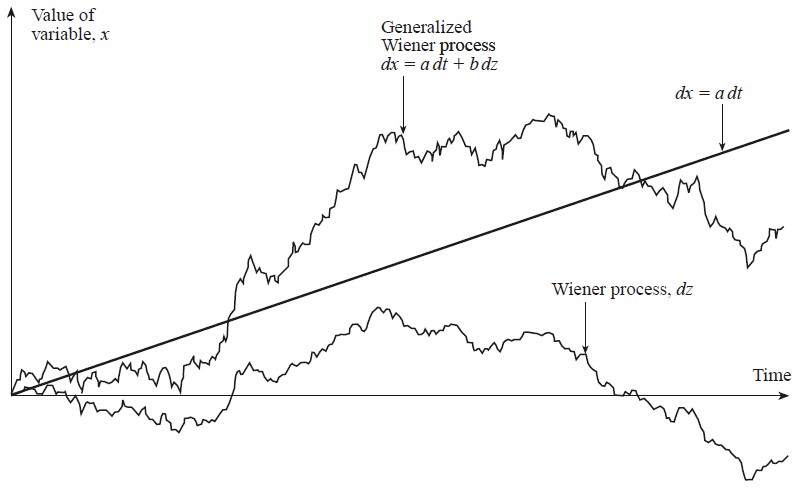
|
股票价格模型
-
伊藤过程(Itô Process):漂移率和方差率为时间
- 随机微分方程
- 离散化
- 随机微分方程
-
广义维纳过程不是合适的股票价格模型
- 漂移率和方差率为常数的假设不合理
- 股票价格可能为负
- 可假设漂移率和方差率与股票价格成正比
-
几何布朗运动(Geometric Brownian Motion)
伊藤引理(Itô's lemma)
-
若
- 普通微积分中的链式法则(chain rule)
- 随机微积分的链式法则
- 普通微积分中的链式法则(chain rule)
-
伊藤引理:若随机过程
则随机过程
伊藤引理的极简推导
|
|
伊藤引理的极简推导(续)
伊藤引理的作用和应用
|
主要作用
|
应用举例
|
股票价格分布
- 假设在一段较短时间
- 令
-
连续复利收益率
-
如果
-
-
预期收益率
- 股票价格的预期值是
- 股票的预期收益率是
- 原因是
- 股票价格的预期值是
-
波动率
-
波动率的概念
- 波动率是指1年内连续复利收益率的标准差
- 短时间段
-
估计波动率
- 取时间间隔为
- 计算每个时间间隔的连续复利收益率:
- 计算
- 取时间间隔为
-
波动率的性质
- 交易时段的波动率通常比收盘后要大得多
- 因此,在对期权估值时通常以"交易日"而非日历日来计量时间
- 对于大多数资产假设一年中有252个交易日
The Black-Scholes-Merton定价模型

|
|
Black-Scholes-Merton偏微分方程的推导过程
- 股票和衍生工具价格分别满足
-
- 建立(无风险)组合
- 衍生工具:
- 股票:
- 衍生工具:
- 组合的初始价值及价值变化量
-
- 组合无风险(获得瞬时无风险收益)
-
Black-Scholes-Merton偏微分方程
- 任何价格依赖于股票价格的证券都满足该微分方程
- 不同证券(衍生工具)对应不同边界条件
- 在远期合约中,边界条件是:当
- 该方程的解为:
Black-Scholes-Merton期权定价公式及其性质
|
Black-Scholes公式的性质
|
理解Black-Scholes期权定价公式
|
Black-Scholes公式可整理为: 其中:
|
|
希腊字母(Greeks)
将期权价格泰勒展开:
| 希腊字母 | 公式 | 风险指标定义 | 主要应用场景 |
|---|---|---|---|
| Delta | 期权价格对标的资产价格 变化的敏感度 |
1. 方向性风险管理 2. 构建Delta中性策略 3. 确定对冲比率 4. 评估期权实值/虚值程度 |
|
| Gamma | Delta对标的资产价格 变化的敏感度 |
1. 评估大幅波动风险 2. 设计波动性交易策略 3. 决定Delta对冲再平衡频率 4. 控制凸性风险敞口 |
|
| Theta | 期权价格对时间 流逝的敏感度 |
1. 设计时间价值衰减策略 2. 优化期权持有期 3. 规划期权展期时机 4. 收益率计算和时间套利 |
|
| Vega | 期权价格对隐含波动率 变化的敏感度 |
1. 波动率风险管理 2. 设计波动率交易策略(跨式/宽跨式) 3. 监控市场情绪变化 4. 评估波动率偏斜交易机会 |
|
| Rho | 期权价格对无风险利率 变化的敏感度 |
1. 利率风险评估 2. 长期期权管理 3. 设计跨市场套利策略 4. 期权与固定收益产品组合管理 |
不常见期权希腊字母列表
| 希腊字母 | 公式 | 定义 | 主要用途 |
|---|---|---|---|
| Epsilon | ∂V/∂r* | 期权价格对标的资产股息率变化的敏感度 | 股息政策变更风险管理,除息日前后策略调整 |
| Lambda | (∂V/∂S)×(S/V) | 期权价格变化与标的价格变化的弹性比率 | 评估期权杠杆效应,资本效率分析 |
| Vomma (Volga) | ∂²V/∂σ² | Vega对波动率变化的敏感度 | 波动率的波动率(vol-of-vol)风险管理 |
| Vanna (DvegaDspot) | ∂²V/∂S∂σ | Delta对波动率变化的敏感度 | 评估价格和波动率交互效应 |
| Charm (DdeltaDtime) | ∂²V/∂t∂S | Delta随时间的变化率 | 管理假日效应,临近到期日Delta调整 |
| Color (DgammaDtime) | ∂³V/∂t∂S² | Gamma随时间的变化率 | 长假期前的Gamma风险重新评估 |
| Speed | ∂³V/∂S³ | Gamma对标的资产价格变化的敏感度 | 极端市场条件下的风险控制 |
| Zomma | ∂³V/∂S²∂σ | Gamma对波动率变化的敏感度 | 波动率环境变化下的Gamma调整 |
| Veta (DvegaDtime) | ∂²V/∂t∂σ | Vega随时间的变化率 | 管理长期波动率交易的时间衰减 |
| Vera (DvegaDr) | ∂²V/∂r∂σ | Vega对利率变化的敏感度 | 评估利率与波动率的交互影响 |
| Ultima | ∂²V/∂σ³ | Vomma对波动率变化的敏感度 | 极端波动率环境的风险评估 |
| Dual Delta | ∂V/∂K | 期权价格对行权价变化的敏感度 | 期权产品设计和行权价优化 |
| Dual Gamma | ∂²V/∂K² | Dual Delta对行权价变化的敏感度 | 复杂期权产品的行权结构设计 |
认股权证与可转换债券
-
认股权证(Warrants) 是公司以自己的股票作为标的发行的长期看涨期权
- 认股权证通常在发行债券的时候被创造出来
- 认股权证通常与债券分开交易
- 当认股权证被执行时,发行人对持有人结清
- 当认股权证被执行时,公司获得现金同时发行新的股票
-
可转换债券(Convertible bonds) 是公司发行的,在特定时间可以按照事先确定的转换比率转换为股票的债券
- 可转换债券等价于普通债券加认股权证
- 可转换债券使公司可以以较低的票息率发行债务
定价
认股权证和可转债可以用标准的期权定价模型定价,我们只需将摊薄效应(dilution effect)考虑在内。假设公司现有
在新股摊薄之后:
简化后,我们得到:
这等于
指数期权
|
|
期货期权
|
|
期权定价的扩展模型:随机波动率模型
-
核心理念
- 放弃波动率恒定假设
- 波动率本身遵循随机过程
- 符合市场观察到的波动率聚集现象
-
Heston模型(Heston, 1993)
-
SABR模型(Hagan et al., 2002)
- 带杠杆效应的随机alpha-beta模型
- 利率衍生品市场标准
-
Hull-White模型(Hull and White, 1987)
- 波动率遵循对数正态分布
-
随机波动率模型优势
- 准确复制波动率微笑/偏斜现象
- 捕捉波动率的均值回归特性
- 考虑波动率与资产价格的相关性
- 提高长期期权定价准确性
期权定价的扩展模型:跳跃扩散模型
-
核心理念
- 在连续扩散过程中加入离散跳跃成分
- 模拟市场中的突发事件和极端价格变动
- 反映市场中实际存在的尾部风险
-
Merton跳跃扩散模型(Merton, 1976)
-
Kou双指数跳跃模型(Kou, 2002)
- 跳跃幅度遵循不对称双指数分布
- 区分上行和下行跳跃
-
Bates模型(Bates, 1996)
- 结合Heston随机波动率与跳跃过程
- 同时捕捉连续波动与离散事件
-
跳跃扩散模型优势
- 能够刻画市场崩盘等极端事件
- 改善短期期权的定价准确性
- 生成更符合实际的尾部分布
- 适用于市场震荡期的风险管理
期权定价的扩展模型:长记忆过程模型
-
核心理念
- 考虑资产回报的长期依赖性
- 打破了马尔可夫假设
- 过去的价格变动对未来有持久影响
-
分数布朗运动模型
-
FIGARCH模型(Baillie et al, 1996)
- 分数积分GARCH
- 捕捉波动率的长期记忆
-
Rough波动率模型(Gatheral et al., 2018)
- 使用粗糙路径描述波动率动态
-
长记忆过程模型优势
- 捕捉市场中观察到的长期依赖性
- 改善长期期权的定价
- 符合波动率的实证观察结果
- 适合大宗商品和低流动性市场
期权定价的扩展模型:其他重要扩展模型
|
|
期权定价的数值方法
| 方法 | 基本原理 | 优点 | 缺点 | 应用场景 |
|---|---|---|---|---|
| 二叉树模型 (Binomial Tree) |
将价格变动离散化为上涨/下跌两种可能,从期满日倒推定价 | 直观易懂,适合美式期权 | 简单期权结构,早期行权分析 | |
| 有限差分法 (Finite Difference) |
将Black-Scholes偏微分方程转化为离散差分方程,通过网格求解边值问题 | 处理复杂边界条件,计算效率高 | 路径依赖期权,复杂边界条件问题 | |
| 蒙特卡洛模拟 (Monte Carlo Simulation) |
通过大量随机模拟计算期权的期望收益 | 适用于高维问题,灵活处理各种随机过程 | 计算量大,对美式期权不够高效 | 多资产期权,路径依赖期权 |
Merton模型与KMV模型:信用风险的期权理论框架
|
Merton模型 (1974)
|
KMV模型
|
实物期权
|
|
课后阅读与练习
课后阅读与练习
-
课后阅读:教材第十一章第三节、十二章第一节、第六章、第七章相关内容
-
练习
- 教材pp186:7,10
- 扫码做题
