L07 远期与期货：定价与估值

基本概念

无套利定价的思想

• 套利策略
  • 低买高卖
  • 不承担风险
  • 不投入资金/资产

• 无套利原理
  • 市场均衡时所有证券都会被正确地定价
  • 所有的套利策略的回报都非正
• 无套利原理的应用
  • 两个组合，如果现在（将来）价值相等，未来（现在）其价值也相等
  • 两个组合，现在（将来）价值大的未来（现在）其价值也更大
  • 两个组合，现在（将来）价值小的未来（现在）其价值也更小

假设与符号

• 假设

  1. 无交易费用
  2. 每个参与者适用的税率相同
  3. 投资者可以以相同的无风险利率投资和融资
  4. 一旦套利机会出现即会被投资者利用

• 符号

  • ：距离远期或期货合约交割日期的时间（年）
  • ：当前时刻远期或期货的标的资产的市场价格
  • ：当前时刻的远期或期货价格
  • ：以连续复利计算的无风险利率

无收益资产远期合约定价

• 例子

  • 一个无股息股利的股票的现价为$40
  • 3个月的远期价格为US$43
  • 1年期的无风险利率为5% (以连续复利计算)

• 存在套利机会吗？如何套利？

• 如果远期价格为US$39呢？

定价公式

• 如何套利？（零投资，低买高卖，获得套利利润）

• 均衡时无套利机会：所有套利方式得到的利润都非正

  • 若远期被低估：买远期卖现货，套利利润为
  • 若远期被高估：卖远期买现货，套利利润为
  • 无套利机会（现货-期货平价定理）：

• 如果卖空不被允许，公式对投资性资产依然成立

  • 拥有资产的投资者仍然可以套利
  • 不拥有资产但拥有投资能力的个人/机构可以卖出套利策略

定价公式：另一种理解（复制）

The big idea： 用含有衍生工具的组合复制标的资产

• 考虑下面两个组合
  • 组合A：一份标的资产
  • 组合B：一份远期协议+时刻价值为的无风险证券

• 由无套利原理知：

已知现金收益资产远期合约定价

例子：

• 一个附息债券，当前价格为$900
• 债券将在4个月后支付利息$40
• 4个月和9个月的无风险利率分别为3%和4%（以连续复利计算）
• 以该附息债券为标的资产的9个月后到期的远期价格为$910（太高） 或$870（太低）时如何套利?

定价公式

• 均衡时无套利机会：所有套利方式得到的利润都非正

• 套利策略
  • 若远期被低估：买远期卖现货，套利利润为
  • 若远期被高估：卖远期买现货，套利利润为
  • 无套利机会：

定价公式：另一种理解（复制）

• 考虑下面两个组合
  • 组合A：一份标的资产
  • 组合B：一份远期协议+与标的资产收益现金流匹配的一组无风险证券+一份时刻价值为的无风险证券

• 标的资产产生现金收益时：无风险证券组合产生相同金额的现金流
• 组合在期末的价值
  • 组合A：一份标的资产，价值为
  • 组合B：无风险证券期末价值为，正好通过远期协议购买标的资产，其价值为
• 由无套利原理知：

已知红利收益率资产远期合约定价

• 均衡时无套利机会：所有套利方式得到的利润都非正
  • 若远期被低估：买远期卖现货，套利利润为：
  • 若远期被高估：卖远期买现货，套利利润为：
  • 无套利机会：

另一种方法

• 考虑下面两个组合
  • 组合A：份标的资产，其所有收益均再投资于该标的资产
  • 组合B：一份远期协议+一份时刻价值为的无风险证券

• 组合在期末的价值
  • 组合A：一份标的资产，价值为
  • 组合B：无风险证券期末价值为，正好通过远期协议购买标的资产，其价值为
• 由无套利原理知：

远期合约的估值

股票指数期货合约及其定价

股指套利

• 当时，套利者买股指卖期货
• 当时，套利者卖股指买期货
• 股指套利涉及到同时交易股指期货以及许多不同的股票
• 股指套利常常由计算机（算法）生成交易
• 有时无法同时进行交易，此时现货与期货价格间的关系不成立

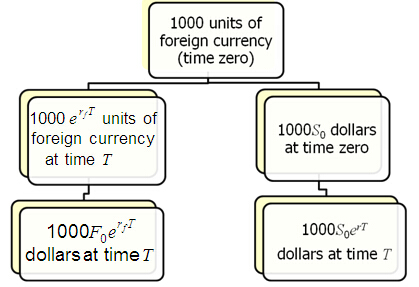
外汇期货合约（货币远期）及其定价

外汇期货合约是指在未来某一特定日期，以约定的价格买入或卖出一定数量某种外汇的标准化合约 外汇类似于产生收益的证券，其收益率为外汇无风险利率（） 外汇期货价格（利率平价关系）： 远期外汇贴水和远期外汇升水 远期外汇贴水： 远期外汇升水：

储存成本

储存成本可以被看做是负的收入（收益率）：

• 若单位时间内的储存成本被表示为资产价值的百分比

  • 对投资性资产：
  • 对消费性资产：

• 若储存成本被表示为成本的现值

  • 对投资性资产：
  • 对消费性资产：

持有成本

• 持有成本(the cost of carry)， ，是储存成本加上利息成本减去获得的收入
  • 对投资性资产：
  • 对消费性资产：

• 一项消费性资产的便利收益率（the convenience yield）
  • 代表持有资产本身的好处
  • 定义：便利收益率（）满足以下关系

远期价格与期货价格

• 通常假设标的资产、到期时间都相同的远期和期货其价格相同

• 理论上，当利息率不确定时，两者有少许差别（为什么会有差别？）：
  • 当利率与资产价格强烈正相关时，期货价格大于远期价格
  • 当利率与资产价格强烈负相关时，期货价格小于远期价格

期货价格与未来现货价格的期望

• 假设投资者对一个资产要求的期望收益率为

• 可以通过以无风险利率投资同时进入一个远期合约多头的方式在未来创造价值为的现金流

• 这说明：
  • 无系统性风险：,
  • 系统性风险为正：,
  • 系统性风险为负：,

课后阅读与练习

课堂练习

• 分析：这是典型的无收益资产远期定价问题

• 解答：

2. 某股票预计在2个月和5个月后每股分别派发1元股息，该股票目前市价等于30，所有期限的无风险连续复利年利率均为6%，某投资者刚取得该股票6个月期的远期合约空头，请问：
   • (a) 该远期价格等于多少？若交割价格等于远期价格，则远期合约的初始价值等于多少？
   • (b) 3个月后，该股票价格涨到35元，无风险利率仍为6%，此时远期价格和该合约空头价值等于多少？

• 分析：
  • (a) 是典型的已知现金收益资产远期合约定价问题
  • (b) 涉及已知现金收益资产远期合约定价和远期合约估值问题

• 解答：
  • (a)

  • (b)

4. A company enters into a forward contract with a bank to sell a foreign currency for at time . The exchange rate at time proves to be . The company asks the bank if it can roll the contract forward until time rather than settle at time . The bank agrees to a new delivery price, . Explain how should be calculated.

• 分析：
  • 这是一个远期设计（定价）问题，实际是一个远期估值问题
  • 在签订新的远期时交易双方不发生支付
  • 新远期协议签订时的价值应等于旧远期协议的价值

• 解答：
  • 时刻旧远期协议多头的价值为：

  • 时刻期货价格应为：

  • 时刻新远期协议多头价值为：

  • 时刻新、旧远期协议价值相等：