-
DNNs的优势:处理"非结构化数据"
- "非结构化数据":图像、文本等
- 输入数据大小可变
- 每个单独的元素(如像素或单词)本身往往没有意义
- DNNs
- 卷积神经网络(CNN)
- 循环神经网络(RNN) 和 Transformer
- 图神经网络(GNN)
- 卷积神经网络(CNN)
- "非结构化数据":图像、文本等
-
DNNs的结构
- 基本单元:人工神经元
- 网络结构:输入层、隐藏层、输出层
神经元细胞与人工神经元
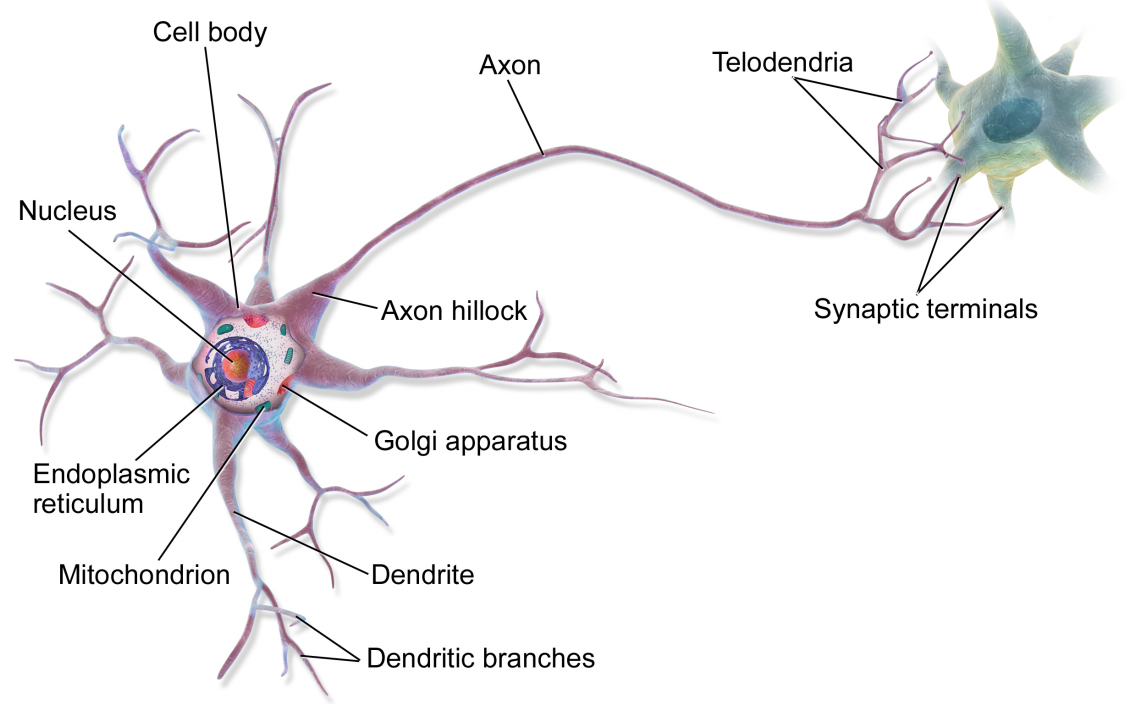
|
|
(非线性)激活函数
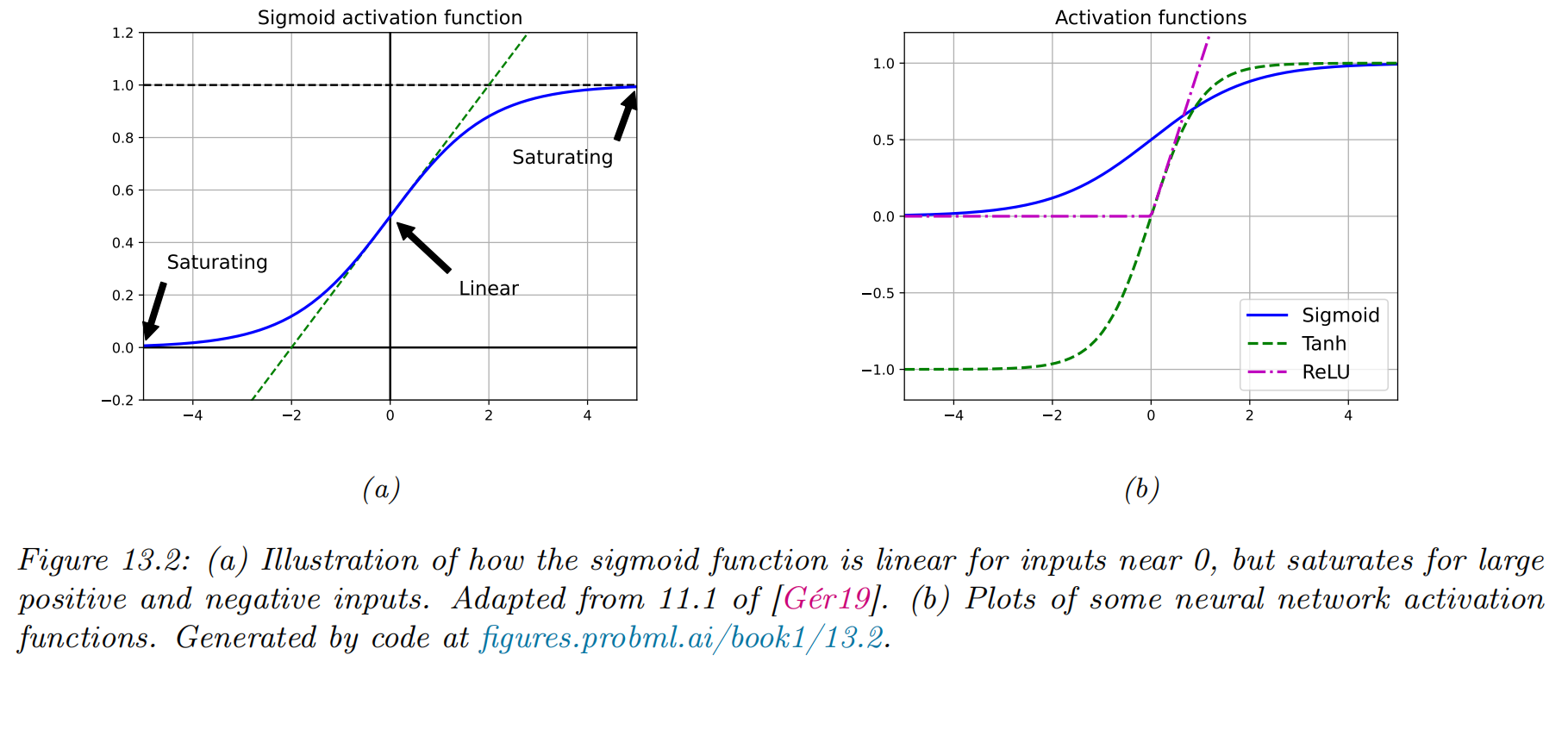
|
|
反向传播算法 (Backpropagation)
|
|
多层感知机(MLP)详细原理
|
全连接前馈神经网络vs卷积神经网络
|
|
卷积
|
|
|
给定一个输入信号序列 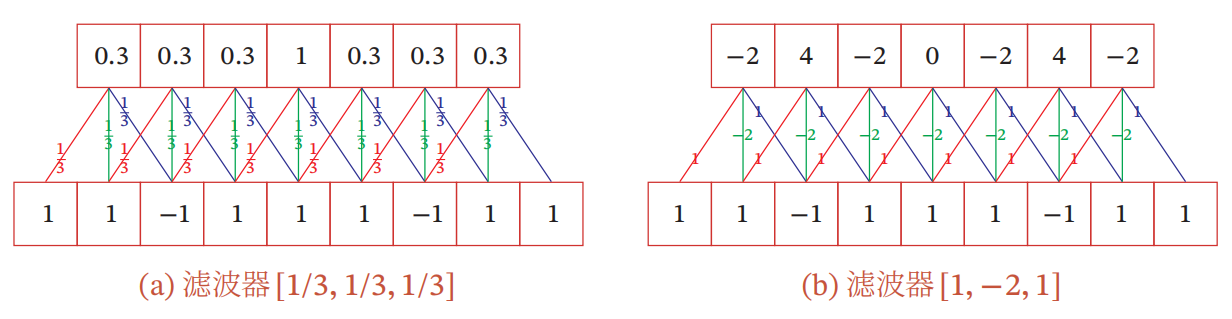
|
|
|
|
|
|
|
|
二维卷积
|
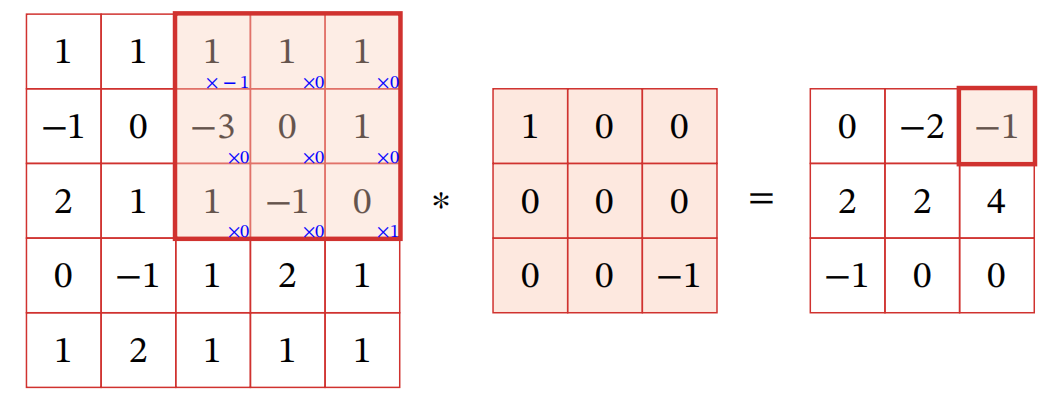
|
|
卷积作为特征提取器 |
互相关 |
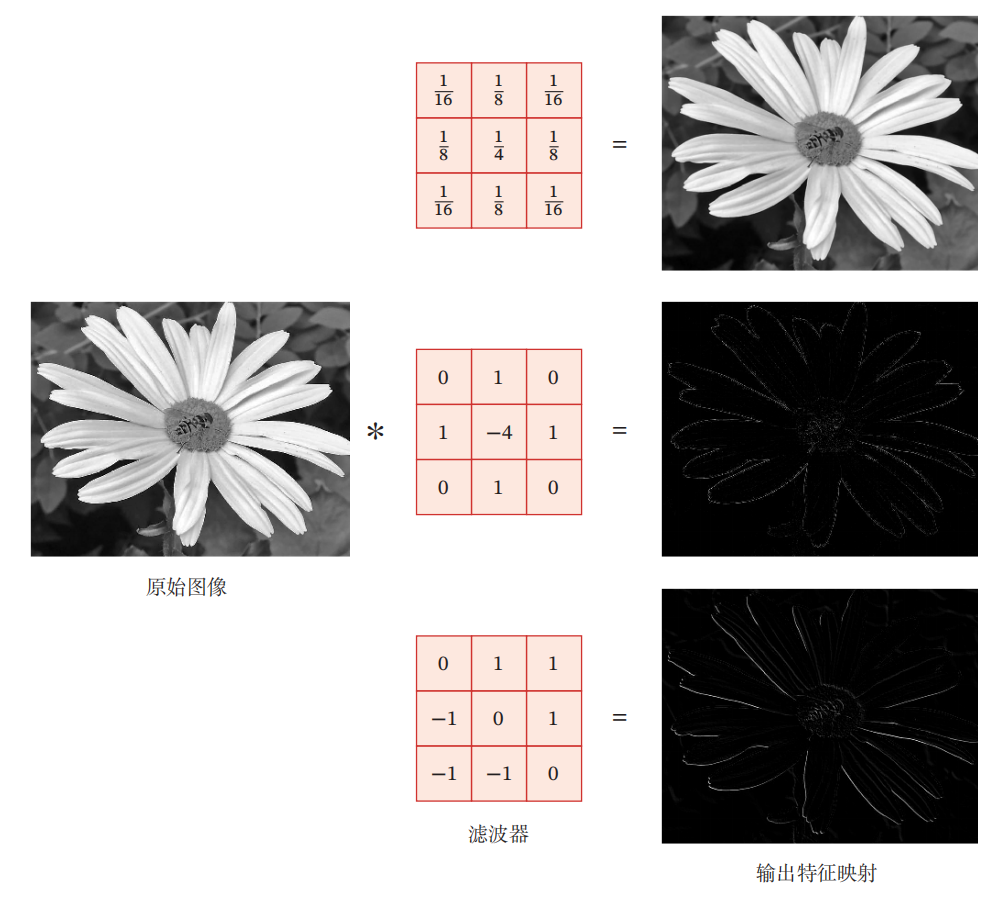
|
|
卷积神经网络 = 卷积层+汇聚层+全连接层
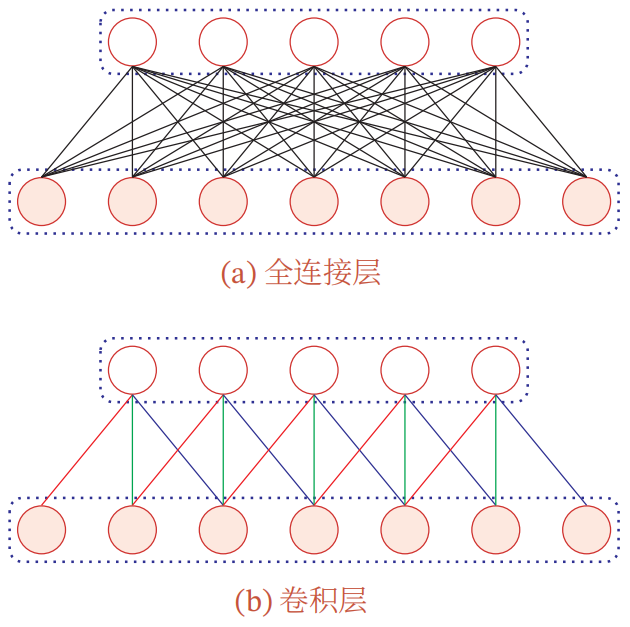
|
|
卷积层的典型结构
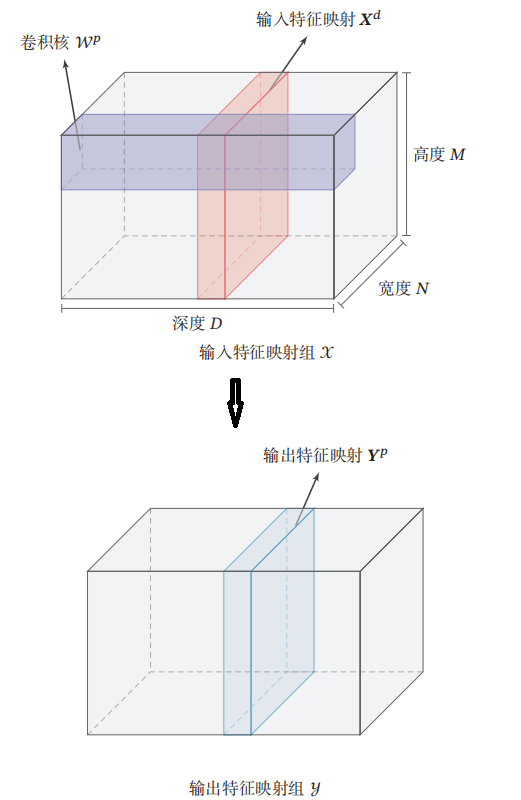
|
|
卷积层的映射关系
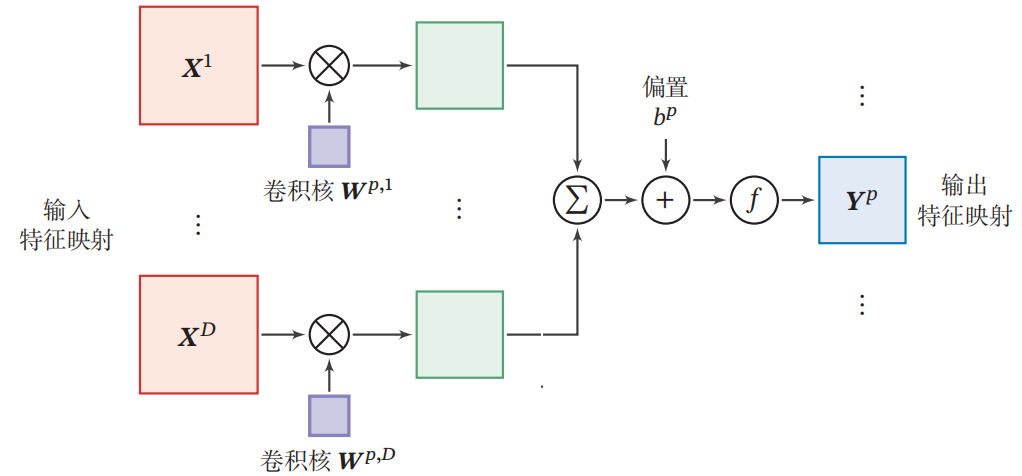
汇聚层/池化层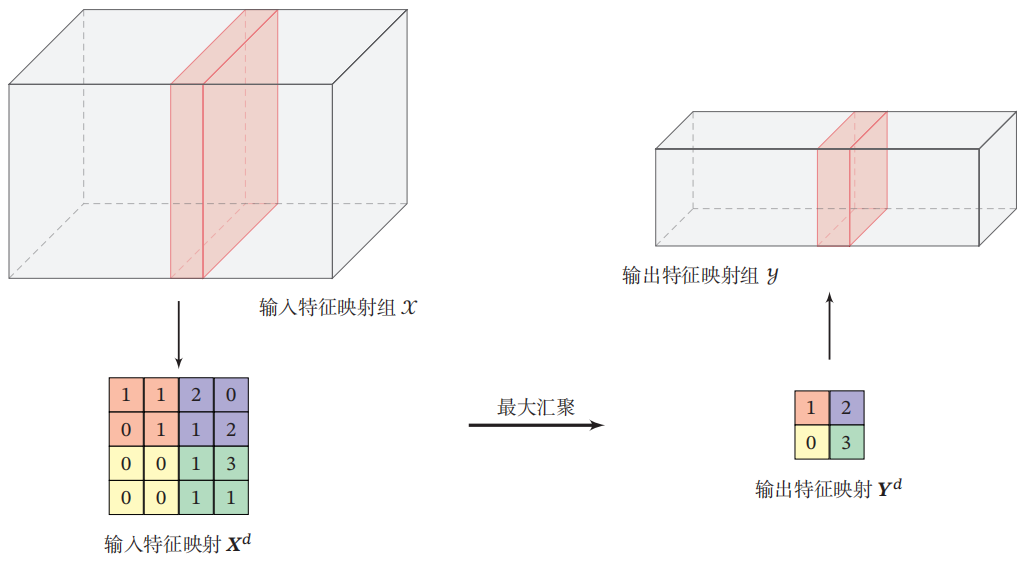
|
|
卷积网络结构
- 卷积网络是由卷积层、汇聚层、全连接层交叉堆叠而成。
- 趋向于小卷积、大深度
- 趋向于全卷积
- 典型结构
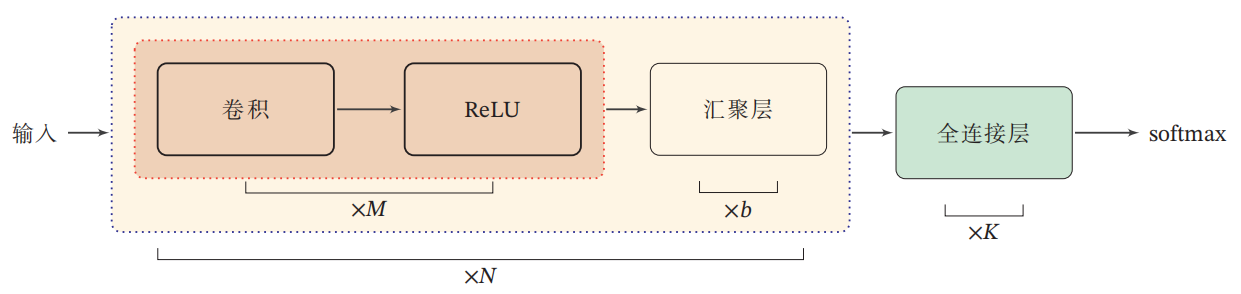
- 一个卷积块为连续
- 一个卷积块为连续
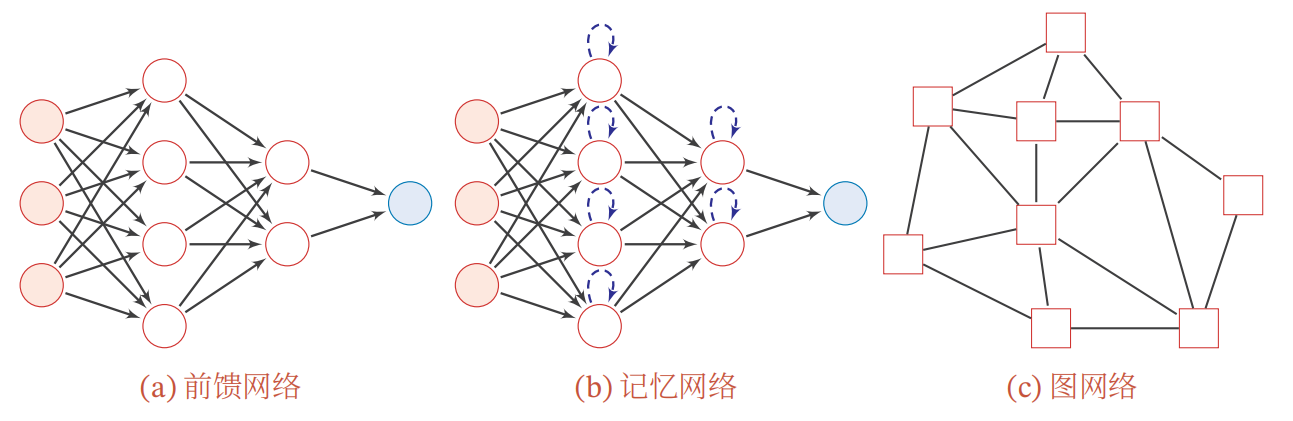
前馈网络
|
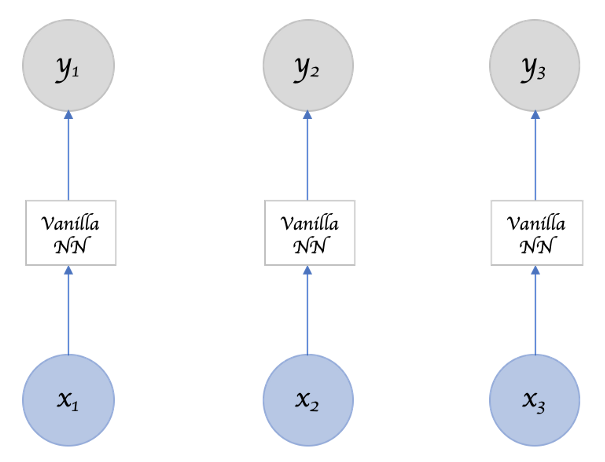
|
可计算问题
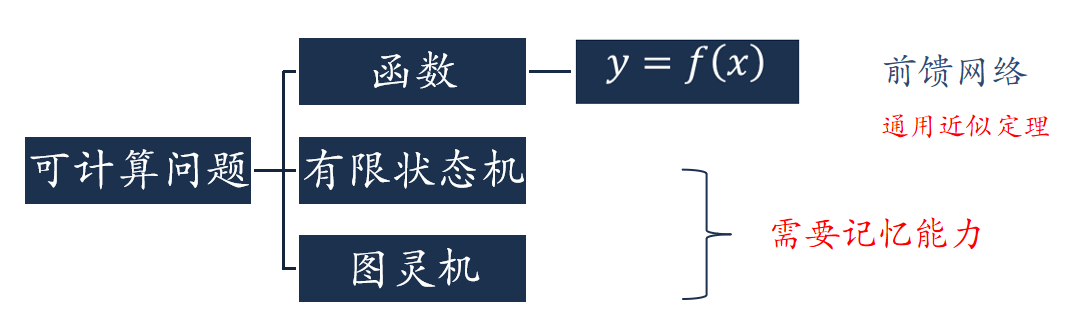
|
|
|
|
给网络增加记忆能力:延时神经网络(Time Delay Neural Network,TDNN)
|
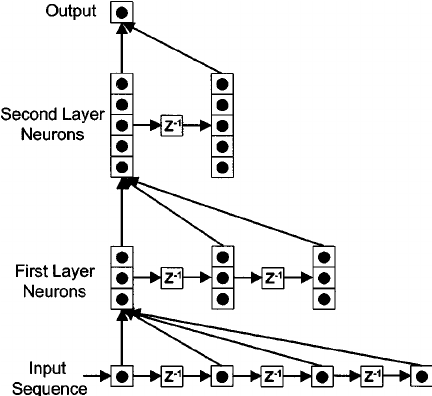
|
给网络增加记忆能力:自回归模型(Autoregressive Model,AR)
- 自回归模型:一类时间序列模型,用变量
- 有外部输入的非线性自回归模型(Nonlinear Autoregressive with Exogenous Inputs Model,NARX)
, - 其中
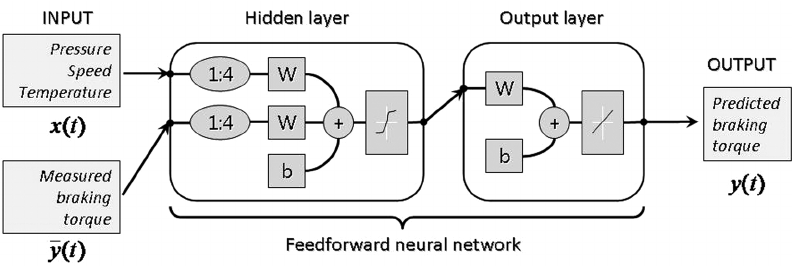
- 其中
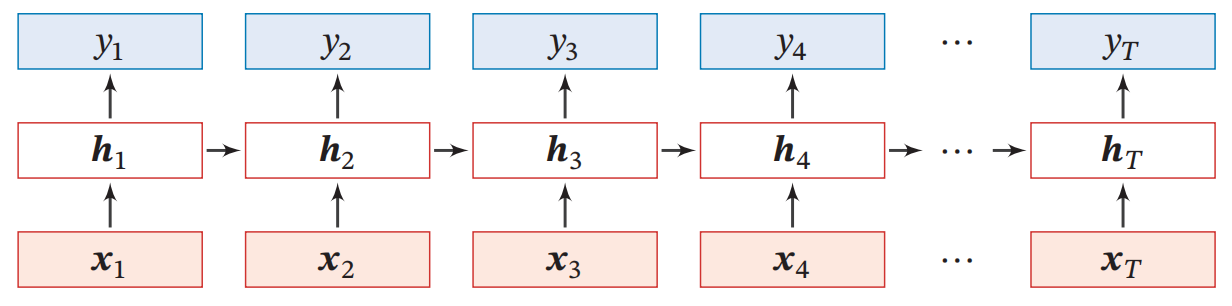
循环神经网络( Recurrent Neural Network ,RNN )
- 循环神经网络通过使用带自反馈的神经元,能够处理任意长度的时序数据。
|
|
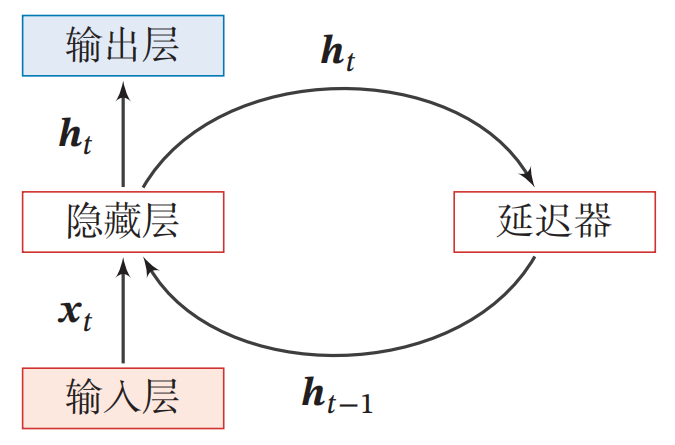
|
- 循环神经网络比前馈神经网络更加符合生物神经网络的结构。
- 循环神经网络已经被广泛应用在语音识别、语言模型以及自然语言生成等任务上
- 作用:
- 输入-输出映射:机器学习模型
- 存储器:联想记忆模型
按时间展开

|
|
简单循环网络( Simple Recurrent Network , SRN )
|
图灵完备
|
长短期记忆神经网络(Long Short-Term Memory, LSTM )
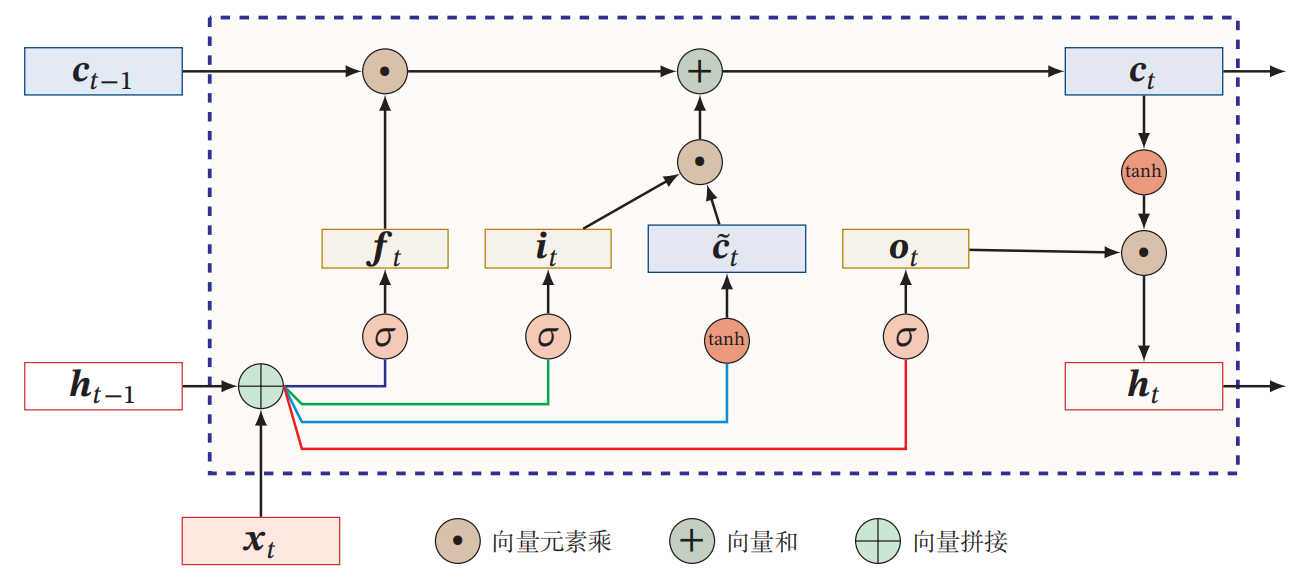
LSTM的各种变体
- 没有遗忘门
- 耦合输入门和遗忘门
- peephole连接
门控循环单元(Gated Recurrent Unit, GRU)
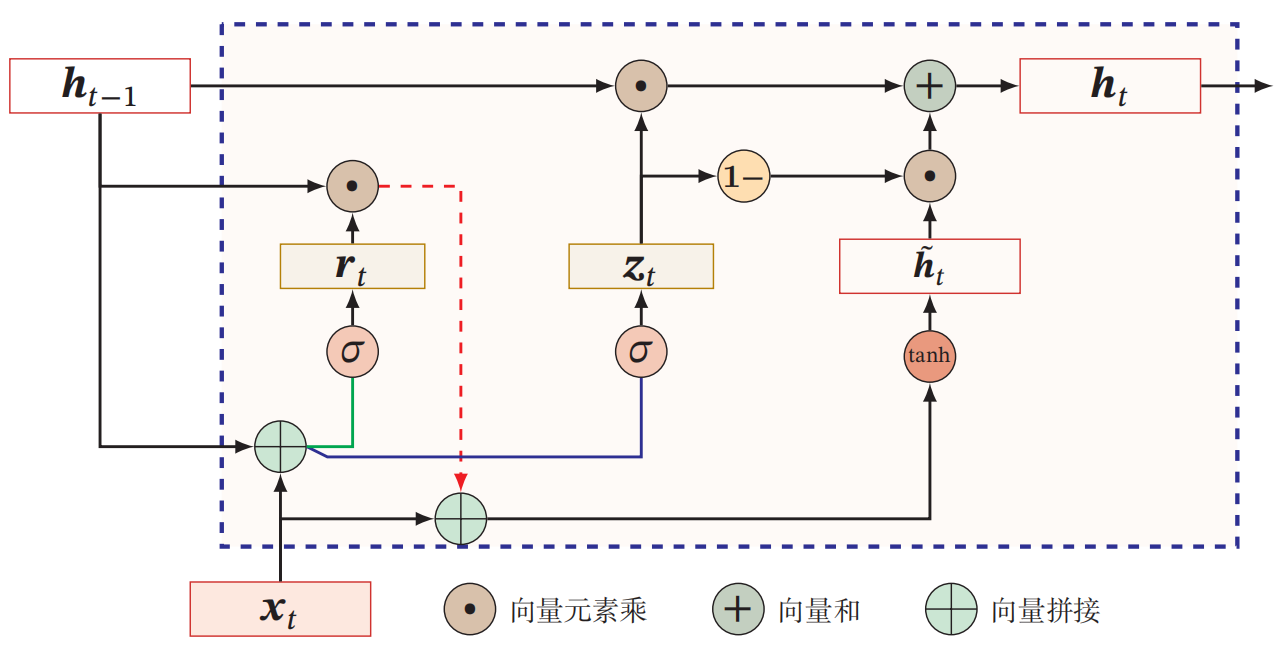
|
|
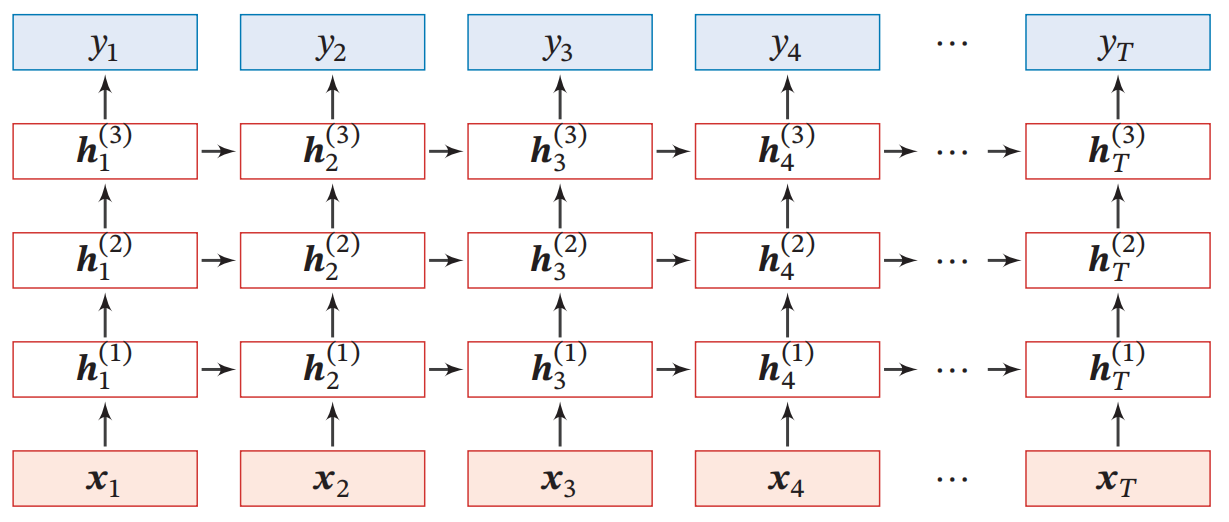
深层模型
堆叠循环神经网络
|
双向循环神经网络
|
|
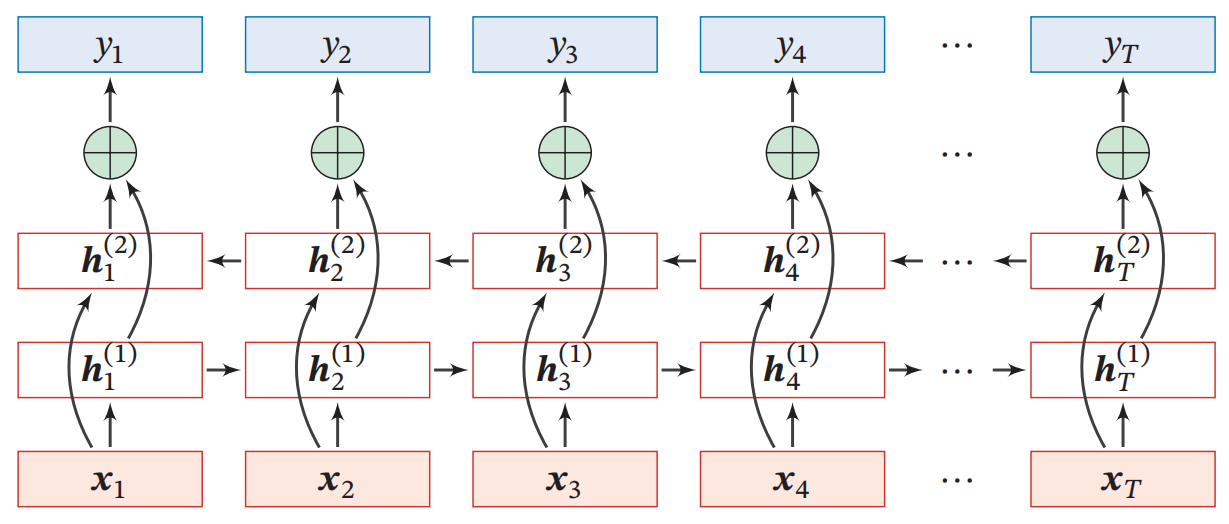
|
生成对抗网络 (GAN)
|
|
GAN实现工具与框架
|
|
深度学习模型比较
| 模型 | 优点 | 局限性 | 典型应用 |
|---|---|---|---|
| MLP | 简单、通用 | 缺乏特征提取 | 分类、回归 |
| CNN | 空间特征提取 | 不擅长序列 | 图像处理 |
| RNN | 序列建模 | 长程依赖 | 时间序列 |
| GAN | 数据生成 | 训练不稳定 | 生成式任务 |
深度学习工具与框架
Python深度学习生态
|
深度学习框架比较
|
强化学习(Reinforcement learning, RL)
|
|
马尔可夫决策过程(MDP)
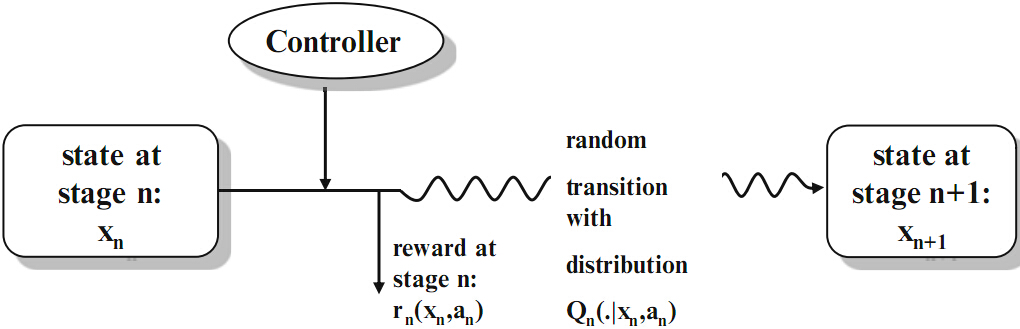
|
|
策略与价值函数
-
策略
-
状态价值函数 (V函数)
-
动作价值函数 (Q函数)
-
最优价值函数
Bellman方程
-
Bellman期望方程
-
Bellman最优方程
强化学习统一更新框架
所有强化学习方法可以视为以下一般形式的特例:
各方法在三个关键维度上有所不同:
- 目标计算(Target的定义)
- 函数表示(值函数的存储方式)
- 更新机制(学习算法)
传统强化学习方法
动态规划(DP)
|
时序差分(TD)学习
|
Q学习
|
深度强化学习:参数化表示
表格表示的局限:
- 无法处理高维状态空间
- 例:金融市场50只股票、10个技术指标 = 500维状态空间
参数化表示的优势:
- 状态价值函数:
- 动作价值函数:
- 策略函数:
金融应用:能够从历史市场数据中泛化到新的市场状态
参数化表示:金融应用
-
金融场景中的目标函数(最大化风险调整后的回报):
-
金融参数化的典型更新过程
- 传统方法:
- 参数化方法:
- 传统方法:
-
金融特定目标:夏普比率、索提诺比率或自定义奖励函数
金融中的简单参数化表示:线性参数化交易策略
-
金融特征
- 价格动量指标 (RSI, MACD)
- 波动率指标 (ATR, 历史波动率)
- 基本面指标 (P/E, P/B, ROE)
- 宏观经济指标 (利率, CPI变化)
-
优势:计算效率高,可解释性强,适合简单交易规则
-
案例:基于技术指标的趋势跟踪交易策略
深度参数化交易模型结构
-
投资组合管理的多层感知机
输入(市场状态) → FC(128) → ReLU → FC(64) → ReLU → FC(资产数量)- 输入:多资产的价格、成交量、波动率等特征
- 输出:各资产的投资权重分配
- 应用:基于每日收盘数据的投资组合再平衡
-
时间序列特化网络
输入(价格序列) → LSTM(128) → LSTM(64) → FC(32) → 交易决策- 优势:捕捉金融时间序列的长期依赖性
- 应用:日内交易、量化策略建模
深度Q网络(DQN)在金融中的应用
- DQN用于期权交易
- 目标计算:
- 状态空间:
- 标的资产价格、波动率曲面、期权希腊字母
- 到期时间、利率环境、市场情绪指标
- 行动空间:
- 离散动作:买入/卖出看涨/看跌期权,构建各种期权组合
- 每个期权策略的仓位大小
- 网络结构:3层MLP (256-128-64)
- 应用场景:波动率套利、Delta中性策略
- 稳定性技巧:目标网络、经验回放(市场历史数据)
- 目标计算:
Deep Deterministic Policy Gradient(DDPG)在金融中的应用
- DDPG用于投资组合优化
-
Actor网络
- 输入:市场状态向量(经济指标、技术指标、基本面数据)
- 输出:各资产的连续投资权重(如 60% 股票, 30% 债券, 10% 黄金)
- 网络结构:FC(400) → ReLU → FC(300) → ReLU → FC(资产数量) → Softmax
-
Critic网络
- 评估当前投资组合配置的预期风险调整回报
- 输出:预期夏普比率或其他风险调整后收益指标
-
目标计算:
-
Proximal Policy Optimization(PPO)在金融中的应用
- PPO用于算法做市
- 状态空间:
- 订单簿深度、买卖价差、交易速率
- 库存水平、市场波动性指标
- 交易对手行为特征
- 策略网络
- 输出:买入/卖出订单的价格和数量分布
- 约束更新保证策略稳定性,避免过度交易
- 价值网络
- 评估当前市场状态下的预期做市收益
- 目标函数:
- 状态空间:
金融特定的复杂参数化设计
-
多时间尺度层次架构
市场数据 → 高频特征(CNN) → 日内特征(LSTM) → 长期特征(Transformer) -
多资产关系建模
- 图神经网络捕捉资产间相关性
- 节点:个股;边:相关性
- 应用:系统性风险评估、对冲策略设计
-
特殊金融应用
- 信用违约风险建模:双向LSTM + 注意力机制
- 高频交易订单执行:3D-CNN处理时空订单簿数据
- 市场微观结构分析:自注意力机制识别订单流模式
金融参数化的特殊挑战与解决方案
- 非平稳性与分布漂移问题
- 解决方案:
- 自适应参数化:根据市场状态动态调整网络结构
- 对抗训练:生成不同市场情景数据
- 元学习:快速适应新的市场环境
- 解决方案:
- 样本稀少性与黑天鹅事件
- 解决方案:
- 基于历史模拟的衍生数据
- 贝叶斯深度学习估计不确定性
- 保守策略优先(避免极端风险)
- 解决方案:
- 可解释性需求
- 基于注意力的资产选择可视化
- 规则嵌入:将金融专业知识编码进网络架构
强化学习算法比较
| 方法 | 函数表示 | 目标计算 | 更新机制 | 模型依赖 | 策略特性 | 稳定性技巧 |
|---|---|---|---|---|---|---|
| 动态规划 | 表格 | 完整模型计算 | 确定性迭代 | 完全依赖 | 在线策略 | 无需 |
| TD学习 | 表格 | 单样本估计 | 增量更新 | 无需 | 在线策略 | 无需 |
| Q学习 | 表格 | 最大化下一步 | 增量更新 | 无需 | 离线策略 | 无需 |
| DQN | 深度网络 | 最大化下一步 | 梯度下降 | 无需 | 离线策略 | 目标网络、回放 |
| DDPG | 双网络 | 策略决定下一步 | 双梯度下降 | 无需 | 确定性策略 | 目标网络、噪声 |
| PPO | 双网络 | 约束策略更新 | 梯度下降 | 无需 | 随机策略 | 梯度裁剪、GAE |
强化学习发展的逻辑
- 共同的理论基础:所有方法都基于MDP和Bellman方程
- 目标一致性:都是通过不同方式近似求解Bellman方程
- 演化路径明确:
- 表格表示 → 函数近似 → 深度网络表示
- 模型依赖 → 无模型学习
- 在线策略 → 离线策略学习
- 简单回溯 → 复杂的目标计算和梯度优化
- 共同挑战的不同解决方案:各方法采用不同技术解决探索-利用、稳定性和泛化问题
参数化表示的核心价值
- 表达能力:能处理金融市场等高维复杂环境
- 泛化能力:从历史数据学习并应用于新市场状态
- 适应性:通过不同网络架构适应不同金融任务需求
- 可扩展性:从简单线性模型到复杂深度架构的自然演进
强化学习领域的发展可以被视为在保持核心原理不变的情况下,通过增强函数表示能力和优化稳定性来解决更复杂金融问题的过程。
强化学习工具与框架
|
|
工具比较
| 工具 | 优点 | 适用场景 | 学习曲线 |
|---|---|---|---|
| OpenAI Gym | 环境丰富 | 算法原型 | 低 |
| Ray RLlib | 分布式 | 大规模学习 | 中 |
| Stable Baselines | 实现简单 | 快速开发 | 低 |
| TF-Agents | 深度集成 | 工业级项目 | 高 |
RL应用举例:最佳执行
- 问题
- 希望在给定时间段内购买或出售给定数量的单一资产的交易者
- 交易者寻求最大化交易执行回报或最小化交易执行成本的策略
(多周期均值-方差)投资组合优化
- 环境
- 市场上
- 投资者在时间 0 进入市场,初始财富为
- 在每个时间点
- 市场上
RL应用举例:期权定价与对冲
- The Black-Scholes Model
- The underlying stock price
- The underlying stock price
-
- the Black-Scholes-Merton partial differential equation
-
- solution
- 强化学习方法
- RL 方法:(深度)Q-learning、PPO 和 DDPG
- 状态:资产价格、当前头寸、期权行使以及到期剩余时间。
- 控制:持股变动
- 奖励
- (风险调整后)预期财富/回报
- 期权收益
- (风险调整后)对冲成本
RL应用举例:做市
- 做市的目标是通过赚取买卖价差来获利,而不积累不必要的大头寸(称为库存)
- 做市商面临三大风险源
- 库存风险:积累不受欢迎的大量净库存的风险,这会因市场波动而显着增加波动性
- 执行风险:限价订单可能无法在期望的范围内得到满足的风险
- 逆向选择风险:存在定向价格变动,席卷做市商提交的限价订单,导致价格在交易期限结束时不会恢复的情况。
RL应用举例:智能投顾
- 随机控制方法
- 框架
- 市场回报的政权转换模型
- 客户和机器人顾问之间的互动机制
- 客户风险偏好的动态模型(即风险规避过程)
- 最佳投资标准
- 机器人顾问与客户反复互动,了解其风险状况的变化
- 智能投顾根据对客户风险厌恶水平的估计,采用有限投资期限的多期均值方差投资标准
- 框架
- 强化学习方法
-
一种探索-利用(Exploration-Exploitation)算法,通过观察投资者在不同市场环境下的投资组合选择来了解投资者随时间的风险偏好
- 状态:各种感兴趣的市场环境的集合被表述为状态空间
- 控制:将投资者的资金放入多个预先构建的投资组合之一
- 状态:各种感兴趣的市场环境的集合被表述为状态空间
-
由两个智能体组成的投资机器人咨询框架
- 反向投资组合优化智能体,使用在线反向优化直接从历史配置数据推断投资者的风险偏好和预期回报
- 深度强化学习智能体,聚合预期收益的推断序列,以制定新的多周期均值-方差投资组合优化问题
-
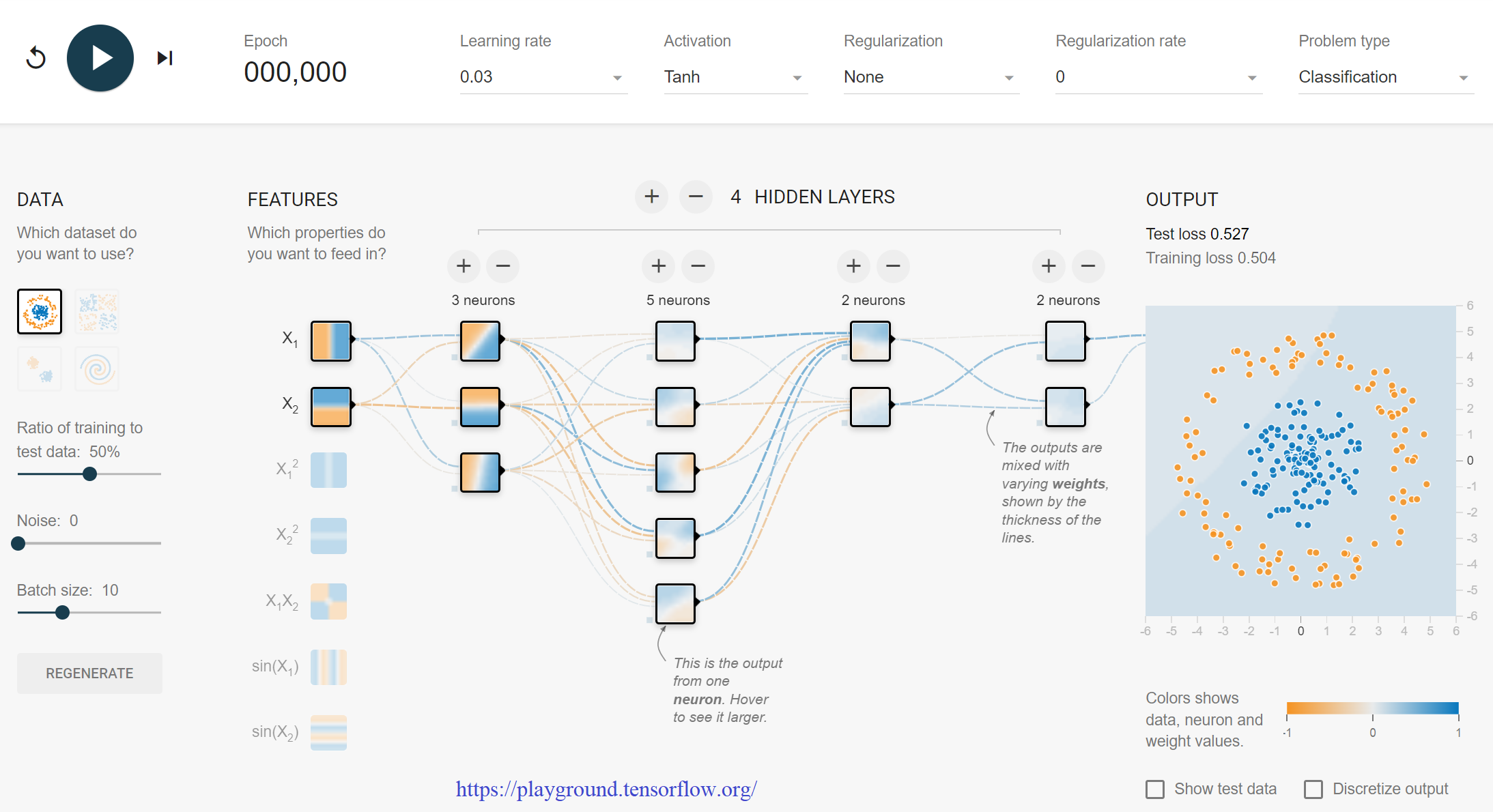
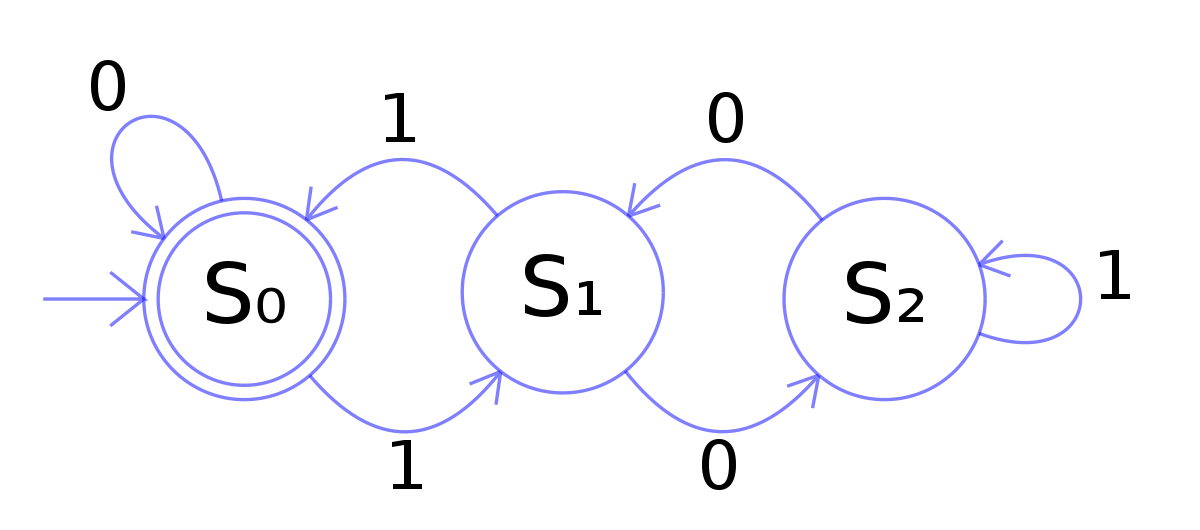
 两个神经网络的对抗性训练
两个神经网络的对抗性训练 核心思想:模仿与欺骗
核心思想:模仿与欺骗 图像生成
图像生成 艺术创作
艺术创作 风格迁移
风格迁移 视频合成
视频合成 数据增强
数据增强 金融风险模拟
金融风险模拟 信用违约预测
信用违约预测 异常交易检测
异常交易检测 合成金融时间序列
合成金融时间序列 PyTorch
PyTorch
 TensorFlow
TensorFlow
 Keras-GAN
Keras-GAN
 GANDLF
GANDLF
 训练不稳定
训练不稳定 模式崩溃
模式崩溃 难以量化生成效果
难以量化生成效果 生成器与鉴别器平衡
生成器与鉴别器平衡